АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Производная по направлению

Читайте также:
  1. ПРОИЗВОДНАЯ
  2. Производная и ее приложения
  3. Производная и её приложение
  4. ПРОИЗВОДНАЯ НЕЯВНОЙ ФУНКЦИИ
  5. Производная по времени от кинетического момента системы свободных материальных точек равна сумме моментов всех внешних сил (главному моменту всех внешних сил).
  6. Тела действуют друг на друга с силами, равными по модулю и противоположными по направлению.
  7. Тема 3.1. Производная функции
  8. Электрический ток, который периодически изменяется по величине и направлению.

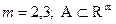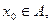
Пусть открыто, , – некоторый вектор

единичной длины. Тогда найдется 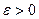такое, что . На множестве

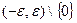рассмотрим функцию , заданную равенством

 

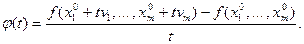
Определение 1. Если существует конечный предел 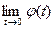, то говорят, что функция имеет в точке 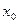производную по направлению . Эта производная обозначается Производная по направлению любого (ненулевого) вектора - это производная по направлению его орта.

Напомним, что координатами орта вектора 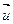являются его направляющие косинусы.

Физический смысл производной по направлению: 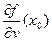характеризует “скорость изменения” функции в точке 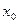вдоль оси, для которой единичный вектор является ортом.

Пусть . Очевидно, .

Теорема 1. Если функция дифференцируема в точке 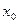, то она имеет производную по любому направлению . При этом

(1)

Напомним, что координатами орта вектора 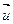являются его направляющие косинусы. Поэтому при нахождении производной по направлению вектора 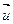в формуле (1) в качестве надо брать направляющие косинусы вектора .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

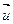Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)