 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Классическая задача на условный экстремум
Классической задачей на условный экстремум принято называть задачу минимизации (или максимизации) функции 
на множестве 
, заданном системой из конечного числа уравнений («связей»).
Пусть рассматривается функция 
двух независимых переменных 
и 
. Допустим, что множество задается одним уравнением:
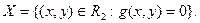
Определение 1. Точка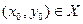 
называется точкой условного локального минимума, если существует такая окрестность 
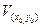этой точки, что для всех 
выполняется неравенство
Определение 2. Точка 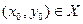называется точкой условного локального максимума, если существует такая окрестность 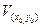этой точки, что для всех
выполняется неравенство
Точки локального условного минимума и локального условного максимума называются точками локального условного экстремума.
Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Этот способ применим в том случае, когда уравнение 
можно разрешить относительно .
Пример 1. Найти точки локального условного экстремума функции
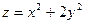(1)
при условии
(2)
Решение. Из уравнения (2) находим, что
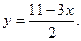(3)
Подставляя (3) в (1), получаем
(4)
У этой функции, заданной на всей числовой оси, есть только минимум (график этой функции есть парабола, ветви которой направлены вверх). Дифференцируя (4) и приравнивая производную к нулю, получаем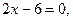 
откуда 
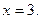При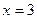 
находим по формуле (3): 
Таким образом, единственной точкой локального условного экстремума задачи (1)-(2) будет точка (3,1), являющаяся точкой локального условного минимума.
В общем случае разрешить уравнение относительно удается не всегда. Для отыскания условного локального экстремума в общем случае используется метод множителей Лагранжа. Для этого составляют функцию
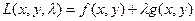
трех переменных 
Эта функция называется функцией Лагранжа, а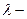 
множителем Лагранжа. Справедлива следующая
Теорема 1. Если точка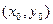 
является точкой локального условного экстремума функции при условии , то существует значение 
множителя Лагранжа, при котором точка 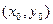есть точка локального экстремума функции
Из Теоремы 1 получаем, что и 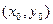удовлетворяют системе 3х уравнений с тремя неизвестными
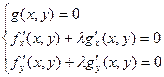. (5)
Из последних двух уравнений системы (5) следует, что в точке 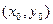векторы 
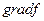и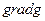 
коллинеарны. Эти градиенты являются нормалями касательных к линиям уровня функций и 
, проходящим через точку 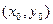. Поэтому в точке условного экстремума линии уровня функций и касаются.
Поиск по сайту: