АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Определение дифференцируемости функции в точке

Читайте также:
  1. I. Определение основной и дополнительной зарплаты работников ведется с учетом рабочих, предусмотренных технологической картой.
  2. II. Основные задачи и функции
  3. III. Определение оптимального уровня денежных средств.
  4. III. Предмет, метод и функции философии.
  5. XVIII. ПРОЦЕДУРЫ И ФУНКЦИИ
  6. А) ПЕРЕДАЧА НА РУССКОМ ЯЗЫКЕ ФУНКЦИИ АРТИКЛЯ
  7. А. Средняя квадратическая погрешность функции измеренных величин.
  8. Абстрактные классы и чистые виртуальные функции. Виртуальные деструкторы. Дружественные функции. Дружественные классы.
  9. Адаптивные функции
  10. Администраторы судов, их функции
  11. Аксиомы науки о безопасности жизнедеятельности. Определение и сущность.
  12. Алгебраическое интерполирование функции.

Пусть 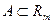, , 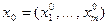- внутренняя точка множества 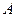. Придадим каждой переменной 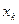приращение 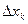и положим . Когда все 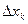достаточно малы, , и мы можем рассматривать полное приращение функции , которое определяется равенством .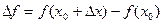

Определение 1. Функция называется дифференцируемой в точке 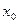, если найдутся числа 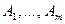такие, что

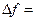
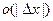, (1)

где 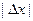= есть расстояние между точкам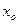и и .

Теорема 1. Если функция дифференцируема в точке 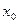, то она непрерывна в точке .

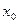Обратная теорема неверна, т.е. непрерывность является необходимым, но недостаточным условием дифференцируемости функции.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)