Упругие волны в стержне

Рис. 2

Применим второй закон Ньютона и закон сложения сил к движению куска стержня, заключенного между двумя плоскостями x и х+∆x. Масса этого куска равна , 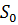где и 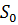– соответственно плотность и сечение в отсутствие деформации. Пусть ξ – смещение центра тяжести рассматриваемого куска. Тогда

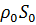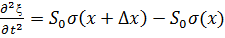∆x (4)

слева стоит произведение массы куска на ускорение его центра тяжести, справа – результирующая внешних сил, действующая на кусок.

Разделим уравнение на 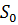∆x:

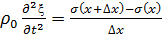(5)

Перейдя к пределу при , получим уравнение

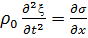(6)

справедливое в каждой точке стержня. Оно указывает, что ускорение данной точки пропорционально частной производной напряжения по x в этой точке.

Подставляя в (9) соотношение (8), получим:

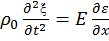(7)

Вспомнив теперь формулу, содержащую определение деформации, и подставив ее в (10), получаем:

(8)

Это—волновое уравнение. Оно указывает, что смещение распространяется но стержню в виде волн

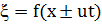(9)

или образует суперпозицию таких волн. Скорость распро­странения этих волн (скорость звука в стержне)

(10)

(мы опускаем для краткости индекс 0 у ρ). Эта скорость тем больше, чем жестче и чем легче материал. Формула (10)—одна из основных формул акустики.

Наряду со смещением нас интересуют скорость 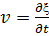, с которой

.движутся отдельные плоскости (не смешивать с u), деформация ε и напряжение σ. Дифференцируя (9) по t и по x, получаем:

(11a)

(11б)

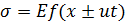. (11в)

Таким образом, смещение, скорость, деформация и напряжение распространяются в виде связанных определенным образом между собой недеформирующихся волн, имеющих одну и ту же скорость и одинаковое направление распространения.

Там, где смещение имеет максимум или минимум, деформация и скорость равны нулю, так как они обе пропорциональны производной

. Физическая интерпретация здесь очевидна: около максимума или минимума смещения соседние (бесконечно близкие) точки одинаково смещены и, следовательно, нет ни растяжения, ни сжатия; в тот момент, когда смещение достигает максимума (минимума), его возрастание сменяется убыванием (или наоборот).

Сравнивая формулы (11а), (11в) и принимая во внимание (10) мы видим, что

(12)

Где

(13)

есть величина, не зависящая от вида функции f и целиком определяемая свойствами материала. Эта величина называется удельным акустическим сопротивлением материала. Она является, как мы видим, наряду с u его важнейшей акустической характеристикой. Название величины 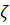связано с формальной аналогией между уравнениями (15) и законом Ома (ρ аналогично разности потенциалов, ν - силе тока).

Поиск по сайту: