АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Уравнение продольных колебаний струны

Читайте также:
  1. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА УРАВНЕНИЕ ТЕПЛОВОГО БАЛАНСА
  2. Алекс встал перед съёмочной группой, надел ремень гитары через голову и поставил руку на струны.
  3. Амплитуда, период, частота, фаза колебаний.
  4. Анализ сезонных колебаний
  5. Анализ сезонных колебаний товарооборота
  6. В декартовых координатах каждая прямая определяется уравнением первой степени с двумя переменными и обратно: каждое уравнение первой степени
  7. Виды колебаний
  8. Внутреннее трение (вязкость) жидкости. Уравнение Ньютона
  9. Волна вероятности. Уравнение Шредингера
  10. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
  11. Вопрос 27: Векторная диаграмма и сложение одинаково направленных гармонических колебаний
  12. Вопрос№15 Механические колебания. Виды колебаний. Параметры колебаний движения

Уравнения продольных колебаний для струны, стержня и пружины записываются одинаково. Рассмотрим стержень, расположенный на отрезке 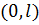оси . Процесс продольных колебаний может быть описан одной функцией представляющий в момент смещение точки, имевший в положении равновесия абциссу 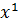. При продольных колебаниях это смещение происходит вдоль стержня. При выводе уравнения будем предполагать, что натяжения, возникающие в процессе колебания, следуют закону Гука.

Подсчитаем относительное удлинение элемента в момент . Координаты концов этого элемента в момент имеют значения:

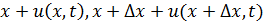
а относительное удлинение равно:

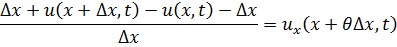
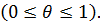
Переходя к пределу при получим, что относительное удлинение в точке определяется функцией . В силу закона Гука натяжение 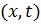равно:

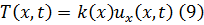
Где 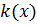-модуль Юнга в точке .

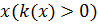Пользуясь теоремой об изменении количество движения, получаем интегральное уравнение колебаний:

 

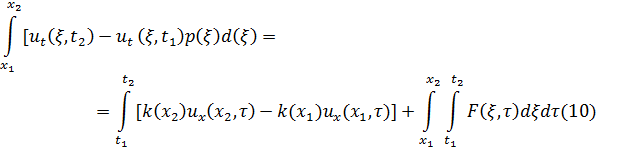
где - плотность внешней силы, рассчитанная на единицу длины.

Предположим существование и непрерывность вторых производных функции . Применяя теорему о среднем и совершая предельный переход при и , приходим к дифференциальному уравнению продольных колебаний стержня:

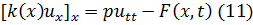
Если стержень однороден , то это уравнение записывают следующим образом:

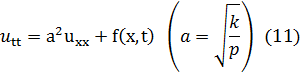
где

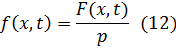
Есть плотность силы, отнесенная к единице массы.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)