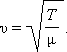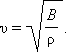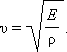|
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Понятие волны. Поперечные и продольные волны
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ»
Технологический институт
Кафедра «Физики, методов контроля и диагностики»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
к курсовой работе
по дисциплине «Теория физических полей»
на тему «Эволюция волны в натянутой струне».
Выполнила:
студент группы ПМКб-11-1
Тадышев А.А
Проверил:
Доктор технических наук
Казаков Р.Х
Дата защиты_____________ Оценка___________
Тюмень 2013г.
Содержание
1. Введение
2. Понятие волны. Поперечные и продольные волны
3. Упругие волны в стержне
4. Упругие волны в газах и жидкостях
5. Стоячая волна
6. Уравнение малых поперечных колебаний струны
7. Уравнение продольных колебаний струны
8. Энергия колебаний струны
9. Вывод
10. Список литературы
Введение
Акустика как раздел физики достигла высокой степени совершенства уже в XIX столетии. XX век был отмечен бурным ростом прикладной акустики, выразившимся в разнообразных технических применений акустических волн и акустической аппаратуры. Развитие это продолжается и сегодня.
Упругими или механическими волнаминазываются механические возмущения (деформации), распространяющиеся в упругой среде. Тела, которые, воздействуя на среду, вызывают эти возмущения, называются источниками волн. Например, зрители в театре слышат речь и пение актеров, звучание музыкальных инструментов, благодаря доходящим до них колебаниям давления воздуха, вызываемых этими источниками звука.
Механические поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных волн.
Понятие волны. Поперечные и продольные волны.
Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной. Процесс распространения колебаний в среде, периодический во времени и пространстве, называется волновым процессом.
По физической форме волны могут быть: механические и электромагнитные. Механические волны бывают разных видов: поперечные и продольные. Если смещение частиц среды происходит в направлении распространения волны, то волна называется продольной. Волны в упругом стержне или звуковые волны в газе являются примерами таких волн. Поперечные волны – это волны, когда смещение колеблющихся точек направлены перпендикулярно скорости распространения волн. В жидкостях и газах упругая деформация сдвига не возникает. Если один слой жидкости или газа сместить на некоторое расстояние относительно соседнего слоя, то никаких касательных сил на границе между слоями не появится. Силы, действующие на границе жидкости и твердого тела, а также силы между соседними слоями жидкости всегда направлены по нормали к границе – это силы давления. То же относится к газообразной среде. Следовательно, поперечные волны не могут существовать в жидкой или газообразной среде. Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой f и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.
Смещение y(x, t) частиц среды из положения равновесия в синусоидальной волне зависит от координаты x на оси OX, вдоль которой распространяется волна, и от времени t по закону:
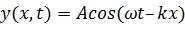 (1)
(1)
где 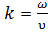 – так называемое волновое число, ω = 2πf – круговая частота.
– так называемое волновое число, ω = 2πf – круговая частота.
На рис.1 изображены «моментальные фотографии» поперечной волны в два момента времени: t и t +Δt. За время Δt волна переместилась вдоль оси OX на расстояние υΔt. Такие волны принято называть бегущими.
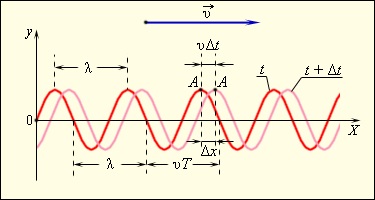
рис.1 бегущая синусоидальная волна в момент времени t и t + Δ t
Длиной волны λ называют расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за период Т, следовательно, λ = υT, где υ – скорость распространения волны. Для любой выбранной точки на графике волнового процесса (например, для точки A на рис. 1) с течением времени t изменяется координата x этой точки, а значение выражения (ωt – kx) не изменяется. Через промежуток времени Δt точка A переместится по оси OX на некоторое расстояние Δx = υΔt. Следовательно:
| ωt – kx = ω(t + Δt) – k(x + Δx) = const или ωΔt = kΔx |
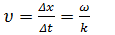 (2) (2)
|
Таким образом, бегущая синусоидальная волна обладает двойной периодичностью – во времени и пространстве. Временной период равен периоду колебаний T частиц среды, пространственный период равен длине волны λ. Волновое число 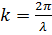 является пространственным аналогом круговой частоты
является пространственным аналогом круговой частоты 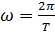 . Обратим внимание на то, что уравнение (1) описывает синусоидальную волну, распространяющуюся в направлении, противоположном направлению оси OX, со скоростью
. Обратим внимание на то, что уравнение (1) описывает синусоидальную волну, распространяющуюся в направлении, противоположном направлению оси OX, со скоростью 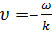 .
.
В бегущей синусоидальной волне каждая частица среды совершает гармонические колебания с некоторой частотой ω. Поэтому, как и в случае простого колебательного процесса, средняя потенциальная энергия, запасенная в некотором объеме среды, равна средней кинетической энергии в том же объеме и пропорциональна квадрату амплитуды колебаний. Отсюда следует, что при распространении бегущей волны возникает поток энергии, пропорциональный скорости волны и квадрату ее амплитуды. Бегущие волны распространяются в средах с определенными скоростями, зависящими от типа волны, а также от инертных и упругих свойств среды.
Скорость поперечных волн в натянутой струне или резиновом жгуте зависит от погонной массы μ (т. е. массы единицы длины) и силы натяжения T:
| |
Скорость распространения продольных волн в безграничной среде определяется плотностью средыρ (т. е. массой единицы объема) и модулемвсестороннего сжатия B, который равен коэффициенту пропорциональности между изменением давления Δ p и относительным изменением объема Δ V / V, взятому с обратным знаком:
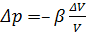 (3)
(3)
Выражение для скорости распространения продольных волн в безграничных средах имеет вид:
|
Например, при температуре 20 °С скорость распространения продольных волн в воде υ ≈ 1480 м/с, в различных сортах стали υ ≈ 5–6 км/с.
При распространении продольных волн в упругих стержнях в формулу для скорости волн вместо модуля всестороннего сжатия B входит модуль Юнга E:
|
Для стали отличие E от B невелико, для других материалов оно может составлять 20–30 % и даже больше.
Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов. Очень похожее явление возникает при звучании духовых инструментов, в том числе органных труб.
Поиск по сайту: