Упругие волны в газах и жидкостях

Мы рассматриваем здесь газ или жидкость (так же как твердое тело в предыдущих параграфах) как сплошную непрерывную среду, отвлекаясь от его атомистической структуры. Под смещением мы здесь понимаем общее смещение вещества, заполняющего объем, заключающий в себе очень много атомов, но малый по сравнению с длиной волны.

Будем считать, что рассматриваемый газ или жидкость находятся в очень длинной цилиндрической трубе, образующие которой параллельны оси х, и что смещение зависит только от одной координаты х. Мы можем применить к столбу газа или жидкости, заполняющему трубу, те же рассуждения, что и к стержню. Мы придем, таким образом, к уравнению

(14)

где р = - σ есть давление в газе или жидкости. Здесь — значение плотности в состоянии равновесия. Пусть ей соответствует давление . Величины , не зависят ни от х, ни от t.

Уравнение (14) применимо и в случае плоских волн в неограниченной жидкой или газообразной среде (можно мысленно выделить цилиндрический столб, параллельный направлению распространения и применить к нему те же рассуждения, что к столбу, заключенному в трубе).

Как известно из термодинамики, р есть функция плотности данной массы газа (или жидкости) и ее температуры. Температура в свою очередь изменяется при сжатии и разрежении. Теплопроводность газов и жидкостей очень мала, поэтому можно считать в первом приближении, что при распространении звука процесс сжатия и разрежения каждой части газа или жидкости происходит адиабатически, т. е. без заметного теплообмена с соседними частями. В термодинамике показывается, что в этом случае (если можно пренебречь внутренним трением и некоторыми другими явлениями) температура является однозначной функцией плотности, и, следовательно, давление также.

При заданной деформации ε в твердом теле также зависит от температуры. Но в акустике твердых тел это обстоятельство не играет существенной роли.

В газах и в жидкостях за некоторыми исключениями (например вода, при температуре ниже 4° С) температура растет при сжатии и уменьшается при расширении.

Есть однозначная функция плотности:

p=f(p). (15)

Введем обозначения

, (16),

Где и 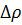- соответственно изменения давления и плотности при нарушении равновесия.

Подставляя первую формулу (19) в (17) и принимая во внимание, что при равновесии давление не зависит от х, т. е.

получаем:

(17)

Найдем теперь связь между и деформацией ε = . Мы сначала выразим через 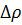, а затем 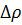через ε:

а) Подставляя (16) в (17), имеем:

разлагая f() в ряд по степеням ,

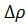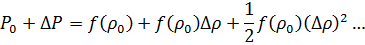
Так как = , то получаем:

(18)

Здесь мы сделаем существенное предположение: будем считать уплотнения и разрежения настолько малыми, что допустимо пренебречь в разложении (21) членами, пропорциональными 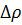, , … и заменить (21) линейным соотношением

Тем самым мы ограничиваем себя исследованием волн малой интенсивности.

—постоянный при данных условиях опыта коэффициент, определяемый состоянием среды при равновесии.

б) Объем в результате деформации превращается в объем

(19)

так как здесь поперечный размер (в отличие от твердого стержня) остается, постоянным, а длина превращается в . Но произведение плотности на объем, равное массе рассматриваемой порции вещества, не меняется:

Подставляя (19) и (22), получаем:

Пренебрегая и здесь высшими степенями малой величины , получаем:

,

Таким образом,

(20)

Мы получаем волновое уравнение

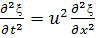(21),

Где . (22)

Отсюда заключаем, что рассматриваемые малые деформации распространяются в виде плоских не деформирующихся волн; скорость распространения (скорость звука) тем больше, чем сильное в данной среде возрастает давление при адиабатическом возрастании плотности; она равна квадратному корню из производной давления по плотности, взятой при значении последней в отсутствие волны (ρ ).

Поиск по сайту: