Уравнение малых поперечных колебаний струны

Каждую точку струны длины можно охарактеризовать значением ее абциссы . Описание процесса колебания струны может быть проведено при помощи задания положения точек струны в различные моменты времени. Для определения положения струны в момент времени достаточно задать компоненты вектора смещения точки в момент .

Мы рассмотрим наиболее простую задачу о колебаниях струны. Будем предполагать, что смещения струны лежат в одной плоскости и что вектор смещения перпендикулярен в любой момент к оси ; тогда процесс колебания можно описать одной функцией , характеризующей вертикальное перемещение струны. Будем рассматривать струну как гибкую упругую нить. Математическое выражение понятия гибкости заключается в том, что напряжение, возникающее в струне, всегда направлены по касательным к ее мгновенному профилю. Это условие выражает с собой то, что струна не сопротивляется изгибу.

Величина натяжения, возникающего в струне вследствие упругости, может быть вычислена по закону Гука. Будем рассматривать малые колебания струны и пренебрегать квадратом по сравнение с единицей.

Пользуясь этим условием, подсчитаем удлинение, испытываемое участком струны . Длина дуги этого участка равна:

Таким образом, в пределах принятой нами точности удлинения участков струны в процессе колебания не происходит;

Рис.5

Отсюда в силу закона Гука следует, что величина натяжения в каждой точке не меняется со временем. Покажем также, что натяжение не зависит и от , т.е.:

Найдем проекции натяжения на оси (обозначим их и ):

,

Где α-угол касательной к кривой с осью . На участок действуют силы натяжения, внешние силы и силы инерции. Сумма проекций всех сил на ось должна быть равна нулю(мы рассматриваем только поперечные колебания). Так как силы инерции и внешние силы по предложению направлены вдоль оси , то:

(1)

Отсюда в силу произвольности следует, что натяжение не зависит от , т.е. для всех значений

(2)

После сделанных предварительных замечаний перейдем к выводу поперечных колебаний струны. Воспользуемся вторым законом Ньютона. Составляющая количества движения участка струны по оси равна:

Где р-линейная плотность струны. Приравниваем изменение количества движения за промежуток времени

импульсу действующих сил, складывающихся из натяжения:

В точках и внешней силы, которую будем считать непрерывно распределенной с плотностью(нагрузкой) рассчитанной на единицу длины. В результате получим уравнение поперечных колебаний элемента струны в интегральной форме:

(3)

Для перехода к дифференциальному уравнению предположим существование и непрерывность вторых производных от . Тогда формулу (3) после двукратного применения теоремы о среднем примет вид:

где

а

Сократив на переходя к пределу при 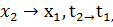получим дифференциальное уравнение поперечных колебаний струны:

В случае постоянной плотности р=const этому уравнению обычно придают вид:

Где

Есть плотность силы, отнесенная к единице массы. При отсутствии внешней силы получим однородное уравнение:

Или

Описывающее свободные колебания струны. Это уравнение является простейшим примером уравнения гиперболического типа.

Если в точке приложена сосредоточенная сила (рис.6)

рис.6

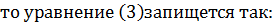
Пользуясь теоремой о среднем, сокращая обе части равенства на и переходя к пределу при , получим:

Отсюда видно, что в точке приложения сосредоточенной силы первые производные претерпевают разрыв и дифференциальное уравнение теряет смысл. В этой точке должны выполнятся два условия сопряжения:

Первое из которых выражает непрерывность струны, второе определяет величину излома струны в точке , зависящую от и натяжения

Поиск по сайту: