Стоячая волна

Если волны, бегущие по струне во встречных направлениях, имеют синусоидальную форму, то при определенных условиях они могут образовать стоячую волну.

Пусть струна длины l закреплена так, что один из ее концов находится в точке x = 0, а другой – в точке x ₁ = L (рис. 2.). В струне создано натяжение T.

Рис. 3. Образование стоячей волны в струне, закрепленной на обоих концах

По струне одновременно распространяются в противоположных направлениях две волны одной и той же частоты:

• – волна, бегущая справа налево;
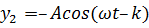• – волна, бегущая слева направо.

В точке x = 0 (один из закрепленных концов струны) падающая волна y ₁ в результате отражения порождает волну y ₂. При отражении от неподвижно закрепленного конца отраженная волна оказывается в противофазе с падающей. Согласно принципу суперпозиции, который является экспериментальным фактом, колебания, вызванные встречными волнами в каждой точке струны, складываются. Таким образом, результирующее колебание в каждой точке равно сумме колебаний, вызванных волнами y ₁ и y ₂ в отдельности. Следовательно,

(23)

Это и есть стоячая волна. В стоячей волне существуют неподвижные точки, которые называются узлами. Посередине между узлами находятся точки, которые колеблются с максимальной амплитудой. Эти точки называются пучностями.

Оба неподвижных конца струны должны быть узлами. Приведенная выше формула удовлетворяет этому условию на левом конце (x = 0). Для выполнения этого условия и на правом конце (x = L), необходимо чтобы kL = n π, где n – любое целое число. Это означает, что стоячая волна в струне возникает не всегда, а только в том случае, если длина L струны равняется целому числу длин полуволн:

(24)

Набору значений λ _n длин волн соответствует набор возможных частот f_n:

где 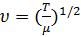– скорость распространения поперечных волн по струне. Каждая из частот и связанный с ней тип колебания струны называется нормальной модой. Наименьшая частота f ₁ называется основной частотой, все остальные (f ₂, f ₃, …) называются гармониками. На рис. 2 изображена нормальная мода для n = 2.

В стоячей волне нет потока энергии. Колебательная энергия, заключенная в отрезке струны между двумя соседними узлами, не транспортируется в другие части струны. В каждом таком отрезке происходит периодическое (дважды за период T) превращение кинетической энергии в потенциальную и обратно как в обычной колебательной системе. Но в отличие от груза на пружине или маятника, у которых имеется единственная собственная частота струна обладает бесконечным числом собственных (резонансных) частот . На рис. 3 изображены несколько типов стоячих волн в струне, закрепленной на обоих концах.

Рис.4

В соответствии с принципом суперпозиции стоячие волны различных типов (т. е. с разными значениями n) могут одновременно присутствовать в колебаниях струны.

Поиск по сайту: