Векторлык алгебра

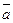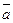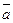Вектор деп бағытталған кесіндіні айтады, яғни кесіндінің белгілі бір ұзындығы және бағыты болады. Егер А – вектордың басы, ал В –вектордың ұшы болса, онда вектор немесе символымен белгіленеді. векторы векторына қарама-қарсы вектор деп аталады (оның басы В нүктесінде, ал ұшы А нүктесінде орналасқан). векторына қарама-қарсы векторды деп белгілейді. векторының ұзындығы немесе модулі деп кесіндісінің ұзындығын айтады және оны немесе деп белгілейді. Ұзындығы нөлге тең векторды нөлдік вектор деп атайды және ол деп белгіленеді. Нөлдік вектордың бағыты анықталмаған.

Ұзындығы бірге тең векторды бірлік вектор деп атайды және оны деп белгілейді. Егер бірлік вектордың бағыты 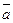векторының бағытымен сәйкес келсе, онда ол 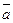векторының орты деп аталады және деп белгіленеді.

Параллель түзулерде немесе бір түзудің бойында жататын векторлар коллинеар векторлар деп аталады және 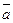|| 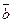деп белгіленеді. Коллинеар векторлар бағыттас болуы да, қарама-қарсы бағытта да болуы мүмкін.

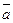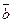Егер екі және векторлары коллинеар болып, бағыттас және ұзындықтары бірдей болса, онда оларды тең векторлар (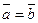) дейді. Тең векторлар еркін векторлар деп те аталады. Бұл векторлардың басты нүктесін кеңістіктегі кез келген нүктеге көшіруге болады.

Егер кеңістіктегі үш вектор бір жазықтықта немесе параллель жазықтықтарда жатса, онда олар компланар векторлар деп аталады.

Векторларға қолданылатын сызықтық амалдар

Сызықтық амалдар деп, векторларды қосу және алу, векторды санға көбейту амалдарын айтады.

Екі вектордың қосындысын екі жолмен табуға болады: бірі параллелограмм әдісі, екіншісі үшбұрыштар әдісі.

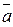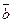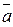Параллелограмм әдісі. және векторларының қосындысы деп, және 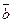векторларының ортақ бас нүктесінен шығатын, параллелограммның диагоналіне тең болатын векторды айтады.

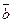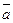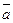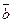Үшбұрыштар әдісі. Егер векторының басы векторының ұшына орналасса, онда және векторларының қосындысы деп, 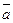векторының басы мен 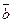векторының ұшын қосатын векторды айтады.

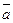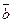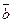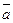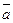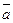Бір нүктеден шығатын және векторларының айырымы деп векторының ұшын векторының ұшымен қосатын векторды айтады. -ға тең, векторына коллинеар, егер болса векторымен бағыттас және 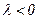болса, 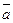векторына қарама-қарсы бағытталған векторын айтады.

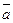және 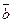векторларының коллинеарлығының қажетті және жеткілікті шарты:

Векторлардың сызықты тәуелділігі. Базис векторлар жүйесі берілсін. векторлар жүйесі үшін бәрі бірдей нөлге тең емес және

(3.1)

теңдігін қанағаттандыратын сандары табылса, онда векторларын сызықты тәуелді векторлар деп атайды. Ал егер теңдік тек сандарының барлығы бірдей нөлге тең болғанда ғана орындалса, онда векторлар жүйесі сызықты тәуелсіз деп аталады.

Егер теңдігі орындалатын сандары табылса, онда векторы векторларының сызықты комбинациясы деп аталады.

Теорема. Екі вектор сызықтық тәуелді болуы үшін олардың өзара коллинеар болуы қажетті және жеткілікті.

Бұл теоремадан кез келген коллинеар емес екі вектор сызықты тәуелсіз болады деген қорытынды шығады.

Теорема. Үш вектор сызықты тәуелді болуы үшін олардың компланар болуы қажетті және жеткілікті.

Бұл теоремадан кез келген компланар емес үш вектор сызықты тәуелсіз векторлар жүйесін құрайды деген қорытынды шығады.

Егер жазықтықта кез келген 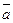векторы үшін нақты сандары табылып, мына теңдік орындалса, онда белгілі ретпен алынған сызықты тәуелсіз векторлар жұбы жазықтықтағы базис деп аталады.

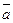Мұндағы сандары векторының базисіндегі координаттары деп аталады да былай белгіленеді: .

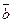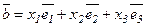Егер кеңістікте кез келген векторы үшін нақты сандары табылып, мына теңдік орындалса, онда белгілі ретпен алынған сызықты тәуелсіз векторлар үштігін кеңістіктегі базис деп атайды.

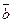Мұндағы сандары векторының базисіндегі координаттары деп аталады да былай белгіленеді: .

Базисті құраушы векторлар базистік векторлар деп аталады.

Осы анықтамалар мен теоремалардан кез келген коллинеар емес екі вектор жазықтықта, ал кез келген компланар емес үш вектор кеңістікте базистік векторлар жүйесі болады деген қорытынды шығады.

Векторды координат өстердің орттары арқылы жіктеу. Вектордың модулі. Кеңістіктегі тік бұрышты декарттық координаталар жүйесін қарастырайық. Ох, Оу, Oz координат өстерінің бойында жатқан бірлік (орт) векторларды сәйкесінше деп белгілейік. Сонда реттелген үштік кеңістікте базистік векторлар жүйесін құрайды. Мұндай, базистік векторлар жүйесін ортогональ базистік жүйе (базис) деп атайды . , себебі үш вектордың қосындысы. Бұл формула вектордың координат өстерінің орттары арқылы жіктелген түрі деп аталады немесе қысқаша деп жазады. Екінші жағынан = , Осыдан болғандықтан - вектордың модулі (ұзындығы).

1-мысал. Егер , онда

Егер 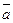векторы Ох, Оу, Oz өстерімен сәйкесінше 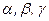бұрыштарын құрса, онда , осыдан

болады. Мұндағы сандары 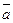векторының бағыттаушы косинустары деп аталады. Алдыңғы өрнекті вектордың модулінің формуласына қойып, теңдігін аламыз.

бірлік векторының коодинаттары екенін оңай байқауға болады. Сонымен, .

2-мысал. векторы үшін

векторлық алгебра осьтегі проекциясы

Бағытталған кесінді деп — “бас нүктесінен” бастап екінші - “соңғы”нүктесіне дейінгі түзу бойындағы нүктелер жиыны.

Жәй мағынасына сәйкес вектор деп бағытталғын кесінді деп түсінуге болады, ал басқа жағдайларда әртүрлі векторлар – белгілі бір эквиваленттік қатынасы бойынша әртүрлі бағытталған кесінділер эквивалентті класстары болып табылады. Бұл эквиваленттік қатынасы әртүрлі болуы мүмкін: ол векторлардың түрін анықтайды (“ еркін ”, “ тұрақты ” т.б.). Басқаша айтқанда, эквивалентті класс ішінде кез келген екі вектор тең болып есептеледі, яғни кез келген вектор сол класты толықтай бейнелей алады.

Еркін векторлар жиыны мен олардың кеңістікті параллель жылжыту жиыны арасындағы изоморфизмды ескерсе, егерде қосу операциясын жылжыту композицияларымен теңестірсе, онда кеңістікті параллель жылжыту жиынын тіпті векторды анықтау үшін де пайдалануғы болады.

Кеңістікті шексіз аз трансформацияларын зерттеуде маңызды рөл атқарады.

· Бaс нүктесі соңғы нүктесімен беттесетін векторды нөлдік вектор деп атайды:

· векторын векторына қарсы вектор деп атайды.

Еркін, сырғанақ және тұрақты векторлар[өңдеу]

Кейде, векторлар ретінде “барлық” тең бағытталған кесінділер жиыны орнына осы жиынның әлдебір өзгертілген түрін (факторжиынын) айтады. Осылайша «еркін» (барлық ұзындықтары мен бағыттары бірдей векторларды бір (толықтай бірдей) деп қарастырады), «сырғанақ» (еркін мағынасы байынша тең векторларды егер бас нүктелері мен соңғы нүктелері бір түзудің бойында жатса) және «тұрақты» векторлар (іс жүзінде бағытталған кесінділердің бас нүктелері әр-түрлі болса – векторлар тең емес деген сөз).

Анықтама. Еркін мен векторлары, егер төртбұрыш мен — параллелограмм болатындай 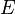және нүктелері табылса, тең болады.

· Ескерту. Анықтаманың күрделенген себебі - нүктелерінің бір түзу бойында жату мүмкіндігінен. Әйтпегенде, оны оңайырақ былай жазуға болар еді:

Анықтама. Еркін бір түзу бойында жатпайтын және векторлары, егер төртбұрыш — параллелограмм болса, тең болады.

Анықтама. Сырғанақ және векторлары, егер * нүктелері бір түзу бойында жатпаса, ал * мен векторлары еркін векторлары ретінде тең болса, онда оларда өзара тең деп аталады.

Қарапайым сөзбен айтқанда, сырғанақ векторларға бағыты мен ұзындығын өзгертпей түзуінің бойымен қозғалуына рұқсат етілген.

· Ескерту. Сырғанақ векторлар әсіресе механикада пайдаланылады. Механикадағы ең қарапайым мысал — күш. Өзі жатқан түзу бойымен вектор бас нүктесін көшіргенмен қай нүктеге қатысты есептесе де күш моменті өзгермейді; керісінше, басын басқа түзуге көшірсе тіпті вектордың бығыты мен ұзындығын сақтағанның өзінде күш моменті әрдайым дерлік өзгереді: сондықтан күшті еркін вектор ретінде санауға болмайды.

Анықтама. Егер сәйкесінше мен , мен нүктелері беттессе, онда тұрақты және векторлары тең деп есептеледі.

Векторларға операциялар қолдану[өңдеу]

Векторларды қосу [өңдеу]

Екі u, v векторлары және олардың қосындысы

Екі векторларды қосуды параллелограмм ережесімен де, үшбұрыш ережесімен де іске асыруға болады.

Үшбұрыш ережесі. Екі мен векторларын үшбұрыш ережесімен қосу үшін осы екі векторды өздеріне біреуінің бас жағы екіншісінің аяғымен беттесетіндей параллель көшіру керек. Сонда пайда болған үшбұрыштың үшінші қабырғасы бас жағы алғашқы вектордың басымен беттесетін бастапқы екі вектордың қосынды векторы болып табылады.

Параллелограмм ережесі. Екі мен векторларын параллелограмм ережесімен қосу үшін екеуін де бастары беттесетіндей параллель көшіріп параллелограммға болықтырады. Сонда екеуінің қосындысы деп параллелограммның осы екі вектор бас жағынан шығатын диагоналін айтады.

Екі сырғанақ векторларды қосу тек қана олар жатқан екі түзу қиылысқанда ғана анықталған. Бұл жағдайда әр вектор өз түзуі бойымен қиылысу нүктесіне дейін көшіріліп, содан кейін параллелограмм ережесімен қосылады.

Екі тұрақты векторларды қосу тек егер олардың ортақ бас нүктесі болғанда ғана анықталған. Бұл жағдайда да олар параллелограмм ережесімен қосылады.

Коллинеар сырғанақ векторларды қосу [өңдеу]

Егер екі сырғанақ векторлар параллель болса, онда қосындыны табу қиыншылығы қосынды вектор жатқан түзуді табудың қиындығында жатыр. (Қосынды вектор бағыты мен ұзындығын еркін векторларды қосқандағыдай анықтаған абзал болар еді) механикада статиканы зерттегенде параллель, еркін векторлармен берілетін, күштерді қосу мәселесінде қосымша гипотеза беріледі: берілген векторлар жүйесіне осы векторлар жатқан түзулерді қиып өтетіндей ұзындықтары бірдей, бағыттары қарама-қарсы бір түзу бойында жататындай екі векторды қосуға болады. Мысалы, параллель түзулерде жататын сырғанақ екі және 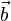внкторларын қосу керек болсын. 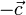Оларға бір түзу бойындағы мен векторларын қосайық. 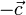мен векторлары жатқан түзулер қиылысады, сондықтан мен векторлары да қиылысады. Яғни, келесі векторлар анықталған

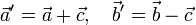
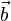мен векторлары жатқан түзулер мен векторлары шамалары бойынша тең бірақ бағыттары қарама-қарсы болғанда ғана қиылыспайды, бұл жағдайда мен векторлары - векторлар жұбы деп аталады.

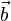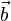Сонымен қорыта айтса, және векторларының қосындысы деп мен векторларының қосындысын түсіну керекі және бұл қосынды мен векторлары жұп болмаған жағдайдың бәрінде дұрыс анықталған.

Векторларды санға көбейту [өңдеу]

векторы мен санының көбейтіндісі леп деп (немесе ) белгіленетін, модулі тең, ал бағыты векторының бағытымен бірдей, егер болса, және керісінше, қарсы бағытталады, егер болса. Егер , немесе вектор нөлдік болса, тек осы жағдайда ғана көбейтінді де — нөлдік вектор.

· Әдетте бұл көбейтіндіні жазғанда бірінші санды сосын векторды жазады, дегенмен де керісінше жазу да қате емес. Қалай десек те, .

Скаляр көбейтінді [өңдеу]

Толық мақаласы: Скаляр көбейтінді

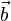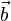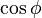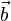мен векторларының көбейтіндісі деп | || | тең санды айтады, мұндағы — мен векторлары арасындағы бұрыш. Белгілеулері: немесе .

Егер векторлардың біреуі нөлдік болса бұрышының беймәлімдігіне қарамастан көбейтінді нөлге тең боп деп есептеледі.

Векторлардың скаляр көбейтіндісінің қасиеттері:

1. — коммутативтілік.

2. — дистрибутивтілік.

3. — санға көбейтуге қатысты сызықтық қасиеті.

4. — вектор нормасы.

Геометриялық түрде алғанда скаляр көбейтінді бір вектордың ұзындығын екінші вектордың біріншісінің бағытына ортогональ проекциясының ұзындығын көбейткенге тең. Кез келген векторының бірлік вектормен скаляр көбейтіндісі векторының сол бірлік векторға ортогональ проекциясы болып табылады.

Векторлық көбейтінді [өңдеу]

Толық мақаласы: Векторлық көбейтінді

a векторынының b векторына Векторлық көбейтіндісі деп келесі шартты қанағаттандыратын c векторын айтады:

· c векторының ұзындығы a мен b векторларының ұзындықтарының және осы векторлардың арасындағы φ бұрышының синусының көбейтінділеріне тең:

· c векторы a мен b векторларының әр-қайсысына ортогональ

· c векотры abc үштігі оң болатындай бағытталған.

Белгілеулер:

Геометриялық мағынасы бойынша векторлық көбейтіндісі векторларына керілген бағатталған параллелограммның ауданы болып табылады.

Аралас көбейтінді [өңдеу]

Толық мақаласы: Аралас көбейтінді

векторларының аралас көбейтіндісі деп векторын 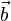және векторларының векторлық көбейтіндісіне скаляр көбейткенге тең скалярды айтады:

(теңдікте скаляр және векторлық көбейтінділер белгілері пайдаланылған).

Кейде аралас көбейтіндіні векторлардың үштік скаляр көбейтінді деп те атайды, нәтижесі скаляр болғандықтан болу керек (дәлірек айтқанда - псевдоскаляр болады).

Геометриялық түрде аралас көбейтіндісі векторларына керілген (бағатталған) параллелепипед көлемі болып табылады.

Векторлардың перпендикулярлық белгісі[өңдеу]

Векторлар сонда, тек сонда, егер олардың скаляр көбейтіндісі нөлге тең болса перпендикуляр болады.

Мысал [өңдеу]

Екі вектор берілген - және . Бұл екеуі теңдігі орындалса ғана өзара перпендикуляр болады.^[1]

Векторлардың коллинеарлық векторлар белгісі[өңдеу]

Егер де бір вектордың абсциссасы екіншісінің абсциссасына қатынасы сәйкес ординаталарының қатынасындай болса бұл векторлар — өзара коллинеар.

Мысал [өңдеу]

Екі вектор берілген - және . Бұл екеуі және 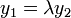, мұндағы , теңдіктері орындалса ғана өзара коллинеар болады.^[2]

Поиск по сайту: