 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Проверка гипотезы о независимости последовательности результатов измерения выборки(первые 20 значений выборки, критерий знаков, критерий трендов, точечный график)
Определение закона распределения и его точечных оценок.
а, б) Округлить значения выборки до сотых и распределить по росту:
Таблица 1: сто значений выборки распределенных по росту (от меньшего к большему)
| -6,69 | -3,61 | -1,89 | -0,85 | -0,34 | 0,44 | 0,73 | 1,14 | 2,2 | 3,9 |
| -5,58 | -3,56 | -1,8 | -0,85 | -0,31 | 0,47 | 0,78 | 1,35 | 2,31 | 4,25 |
| -5,25 | -2,79 | -1,55 | -0,83 | -0,3 | 0,48 | 0,8 | 1,48 | 2,39 | 4,51 |
| -4,94 | -2,63 | -1,53 | -0,83 | -0,22 | 0,49 | 0,82 | 1,53 | 2,54 | 4,53 |
| -4,54 | -2,54 | -1,52 | -0,8 | -0,2 | 0,5 | 0,83 | 1,54 | 3,1 | 4,59 |
| -4,52 | -2,4 | -1,52 | -0,8 | 0,01 | 0,52 | 0,87 | 1,61 | 3,13 | 5,49 |
| -4,03 | -2,36 | -1,51 | -0,73 | 0,08 | 0,52 | 0,88 | 1,79 | 3,23 | 6,29 |
| -3,65 | -2,17 | -1,41 | -0,49 | 0,14 | 0,53 | 0,88 | 1,82 | 3,38 | 6,33 |
| -3,62 | -2,1 | -1,28 | -0,44 | 0,25 | 0,59 | 1,05 | 2,05 | 3,39 | 7,61 |
| -3,61 | -2,08 | -0,94 | -0,4 | 0,35 | 0,59 | 1,08 | 2,19 | 3,79 | 8,85 |
в) Определение размаха или широты измерений:
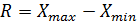 ; (1)
; (1)
R=15,54;
г) Выбор числа разрядов (5-9):
q=7; (2)
д) Определить интервалы(ширина разряда):
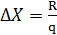 ;(3)
;(3)
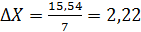 ;
;
| № | Границы интервала | Xjc | nj | Xjc*nj | 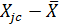
| 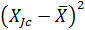
| 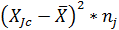
| |
| Xj | Xj+1 | |||||||
| -6,69 | -4,47 | -5,58 | -33,48 | -5,82 | 33,87 | 203,22 | ||
| -4,47 | -2,25 | -3,36 | -36,96 | -3,6 | 12,96 | 142,56 | ||
| -2,25 | -0,03 | -1,14 | -31,92 | -1,38 | 1,9 | 53,2 | ||
| -0,03 | 2,19 | 1,08 | 37,8 | 0,84 | 0,7 | 24,5 | ||
| 2,19 | 4,41 | 3,3 | 39,6 | 3,06 | 9,36 | 112,32 | ||
| 4,41 | 6,63 | 5,52 | 33,12 | 5,28 | 27,88 | 167,28 | ||
| 6,63 | 8,85 | 7,74 | 15,48 | 7,5 | 56,25 | 112,5 |
Середина интервала: 
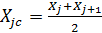 ;
;
Сумма nj :
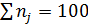 ;
;
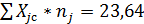 ;
;
Среднее арифметическое:
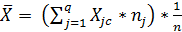 ;
;
n=100;
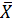 =23,64/100=0,24;
=23,64/100=0,24;
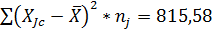 ;
;
Находим значение дисперсии:
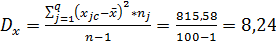 ;
;
Находим значение СКО:
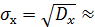 2.87;
2.87;
Находим значение СКО среднего арифметического:
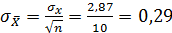 ;
;
По полученным данным строим гистограмму:
Строим кумулятивную кривую
-гистограмма полигона распределения
-кумулятивная кривая
Проверка гипотезы о форме закона распределения размера выборки
| № (j) | Xjc | nj | 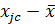
| tj | P(tj) | P(xjс) | nрj | Xj2 |
| -5,58 | -5,82 | -2,03 | 0,0508 | 0,0177 | 3,93 | 1,09 | ||
| -3,36 | -3,6 | -1,25 | 0,1826 | 0,0636 | 14,12 | 0,69 | ||
| -1,14 | -1,38 | -0,48 | 0,3555 | 0,1239 | 27,5 | 0,01 | ||
| 1,08 | 0,84 | 0,29 | 0,3825 | 0,1333 | 29,59 | |||
| 3,3 | 3,06 | 1,07 | 0,2251 | 0,0784 | 17,4 | 1,68 | ||
| 5,52 | 5,28 | 1,84 | 0,0734 | 0,0256 | 5,68 | 0,25 | ||
| 7,74 | 7,5 | 2,61 | 0,0132 | 0,0046 | 1,02 |
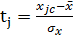 – нормальное отклонение от среднего арифметического;
– нормальное отклонение от среднего арифметического;
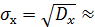 2,87;
2,87;
P(tj) – определяется по таблице «дифференциальная функция нормального распределения»;
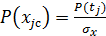 – плотность в серединных интервалах;
– плотность в серединных интервалах;
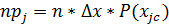 где n=100, Δх=2,22;
где n=100, Δх=2,22;
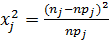 – отклонение;
– отклонение;
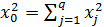 ;
;
Определение числа степеней свободы
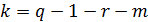 где q=7, r=2(т.к используются
где q=7, r=2(т.к используются 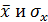 ), m=1 (6,7) если nj<5, то строку объединить с др.
), m=1 (6,7) если nj<5, то строку объединить с др.
k=3;
α=0,1 – уровень значимости;
X02=4,72
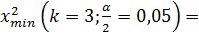 0,352
0,352
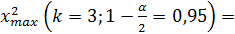 7,815
7,815
0,352<4,72<7,815 – гипотеза о нормальном распределении принимается.
Оценка грубых погрешностей эксперимента.
Xn=7,61 xn=-6,69
Xn+1=8,85 Sx=2,87 xn+1=-5,58
Xu наиб=Xn+1-Xn/Sx=0,43
X0,95=1,0 при n=100
Xu наим=Xn+1-Xn/Sx=0,39
Xu наиб≤X0,95
Xu наим≤X0,95
Оцениваемые результаты являются случайными и отбрасывать их нельзя.
Оценка точности среднего при заданном уровне значимости.
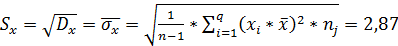 ;
;
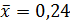 ;
;
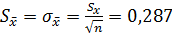 ;
;
Определяем доверенную вероятность
Р=0,9 (90%); α=0,1; Р+α=1
Находим доверительный интервал
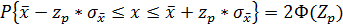 ;
;
По таблице функций Лапласа:
Р=2Ф(Zp)
0,9=2Ф(Zp) Zp=1.65
Ф(Zp)=0,45
Zp – аргумент функции Лапласа отвечающий вероятности Р/2
(0,24-1,65*0,287)≤х≤(0,24+1,65*0,287)
Q=0,24±0.47; Р=0,9
Q – истинное значение измерительной величины
Проверка гипотезы о независимости последовательности результатов измерения выборки(первые 20 значений выборки, критерий знаков, критерий трендов, точечный график)
1) 20 первых значений измерений
| 3,79 | -1,55 | 0,88 | 0,59 |
| -1,52 | -3,65 | -2,1 | 1,61 |
| 0,5 | 5,49 | 0,82 | -0,34 |
| -1,52 | 1,35 | 0,88 | 2,39 |
| -3,61 | 4,59 | 0,08 | 1,08 |
2) 20 первых значений измерений распределенных по росту
| -3,65 | -1,52 | 0,82 | 1,61 |
| -3,61 | -0,34 | 0,88 | 2,39 |
| -2,1 | 0,08 | 0,88 | 3,79 |
| -1,55 | 0,5 | 1,08 | 4,59 |
| -1,52 | 0,59 | 1,35 | 5,49 |
Ме= 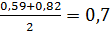
Хj≥Ме +
Хj<Ме -
+- - - - -
-++++ -
++ - - + -
++
r0=9
(r20; 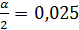 )=15
)=15
(r20; 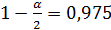 )=6
)=6
Критерий тренда:
Xi>Xj
i=1,2,3……n-1
j=i+1,i+2…..n
j1=17 j11=5
j2=4 j12=0
j3=7 j13=3
j4=4 j14=3
j5=1 j15=1 J0=82
j6=3 j16=1
j7=0 j17=2
j8=12 j18=0
j9=8 j19=1
j10=10
(j20, 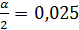 )=125
)=125
(j20, 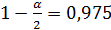 )=64
)=64
Вывод:
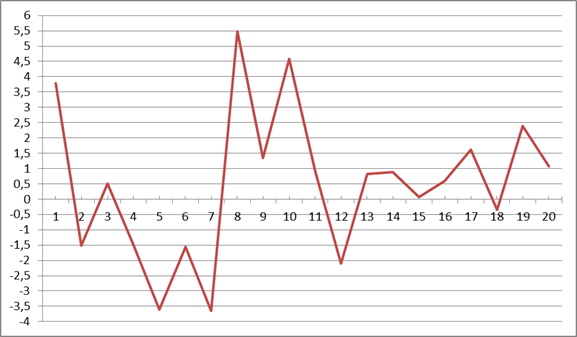
Т.к 64≤82≤125, то J0 – входит в область применения гипотезы. Следовательно гипотеза принимается. Распределение выборки носит случайный характер.
Точечный график
Поиск по сайту: