АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Построить уравнение регрессии

Читайте также:
  1. Абсолютные и относительные показатели силы связи в уравнениях парной регрессии.
  2. Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция
  3. Аппроксимационная задача линейной регрессии
  4. ВИДЫ НЕЛИН.РЕГРЕССИИ И МЕТОДЫ НАХОЖДЕНИЯ ИХ ПАРАМЕТРОВ
  5. Второй закон Ньютона как уравнение движения.
  6. Выбор уравнения регрессии
  7. Выбор формы уравнения множественной регрессии
  8. Гетероскедастичность в уравнениях множественной регрессии, ее признаки и последствия.
  9. Гетероскедастичность в уравнениях множественной регрессии, ее признаки, последствия и методы устранения.
  10. Гетероскедастичность остатков модели регрессии
  11. Гиперболическая и логарифмическая регрессии. Полиномиальная и кусочно-полиномиальная регрессия.
  12. Дифференциальные уравнения движения идеальной жидкости (уравнение Эйлера, вывод)

Вычисление коэффициента корреляции

Для изучения связи между Х и У прежде всего важно нарисовать диаграмму рассеивания, но для установления силы связи в количественных терминах полезно вычислить коэффициент корреляции в соответствии со следующим определением:

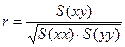- коэффициент корреляции (6.1)

где

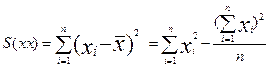- сумма квадратов отклонений по Х (6.2)

 

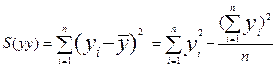- сумма квадратов отклонений по У (6.3)

 

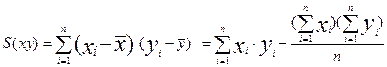- ковариация Х по У (6.4)

Число «n» - это число пар данных, а S(xy) называется ковариацией. Коэффициент корреляции r принимает значения в интервале от -1 до +1. Если абсолютное значение r окажется больше 1, то совершенно ясно, что произошла ошибка и результат нужно пересчитать. В случае сильной положительной связи коэффициент корреляции оказывается близок к +1, а при сильной отрицательной связи достигается значение близкое к -1. Таким образом, когда r близок к 1, это указывает на сильную корреляцию между Х и У, а когда r близок к нулю – на слабую корреляцию. Более того, при r=1 все данные будут лежать на прямой линии. Если вы будете помнить об этом и приучитесь оценивать значение r по диаграмме рассеивания, то сможете обнаруживать ошибки в вычислениях.

При расчете коэффициента корреляции удобно формировать следующую таблицу (табл. 6.2).

Таблица 6.2

Предварительные расчеты

Дата Х У Х2 У2 ХУ
  8,6 0,889 73,96 0,79032 7,6454
  8,9 0,884 79,21 0,78146 7,8676
           
           
           
           
Итого:          

Построить уравнение регрессии

Построить по статистическим данным уравнение регрессии вида , используя следующую очередность этапов:

Этап 1. Найдите по имеющимся данным и .

Этап 2. Подсчитайте S(xx) и S(xy).

Этап 3. Найдите значение по формуле , а по формуле .

Те значения и , которые получаются на этом этапе, доставляют минимум остаточной сумме квадратов.

Этап 4. Сформируйте уравнение регрессии. Постройте график этого уравнения. Проверьте, как «работает» уравнение регрессии путем подстановки исходных данных.


Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)