ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ

Человечество в процессе своего развития использовало различные позиционные системы счисления: пятеричную, десятичную, двенадцатиричную. Создание вычислительной техники привело к необходимости использования систем счисления кратных 2ⁿ: двоичной, восьмеричной, шестнадцатиричной., поэтому возникла необходимость в создании правил перехода чисел из любой позиционной системы в любую другую. В принципе, разработаны различные методики преобразования. Объединим их в 2 подгруппы:

- универсальная;

- частные случаи.

Назовем старую систему, т.е. систему из которой выполняется перевод Р-ичной, а систему в которую он выполняется Q-ичной, тогда универсальная методика перевода чисел из Р-ичной системы в Q-ичную представляется тремя компонентами:

- общий;

- для целых чисел;

- для правильных дробей.

Общая методика:

- представить Р-ичное число двумя операндами, т.е. в виде целой и дробной части (правильной дроби);

- произвести перевод каждого из операндов в новую Q-ичную систему по конкретным правилам;

- сформировать представление числа в новой Q-ичной системе, записав через разделитель полученное изображение целой и дробной части.

Методика преобразования целых чисел (целочисленного операнда):

- разделить на цело Р-ичное число на основание новой Q-ичной системы, записанное в Р-ичном изображении, результат деления: целое число (частное) и остаток;

- зафиксировать остаток и представить его цифрой новой системы;

- проанализировать частное, если оно больше или равно основания системы, то повторить предыдущие пункты, используя частное, как целое число, подлежащее переводу; если частное меньше основания системы, то деление прекратить;

- сформировать результат перевода, как число, старшим разрядом которого является последнее из получаемых частных, а следующие остатки дописать в порядке, обратном получению в виде цифр новой Q-ичной системы.

Универсальное правило перевода правильных дробей:

- умножить переводимую дробь на основание новой системы Q, записанное в старой Р-ичной системе;

- зафиксировать целую часть полученного результата и представить ее цифрой новой системы; проанализировать оставшуюся дробь и если она равна нулю, то прекратить вычисление, в противном случае повторить предыдущие пункты, не переведется нацело, либо до достижения заданной точности (количества зафиксированных цифр;

- сформулировать полученное значение в новой Q-ичной системе структуры: 0,n₁n₂…n_m, где используются в качестве разрядов после разделителя зафиксированные цифры новой системы счисления (n_i) в порядке их получения, т.е. n₁ – результат первого вычисления, n₂ – второго и т.д.

Универсальность методики компенсируется одним недостатком, т.е. неудобством для человека вычислений в любых системах, кроме десятичной. Поэтому на практике универсальным методом пользуются только для перевода чисел из системы с основанием Р=10 в Q-ичную систему с основанием 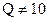. Для обратного перевода чисел из системы 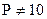в систему Q=10 используют простейший частный случай с методикой:

- представить переводимое число в виде полинома в новом десятичном изображении;

- свернуть полученный полином.

Примеры: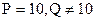

1. 47,4₁₀ перевести в двоичную систему.

47,4₁₀=47₁₀+0,4₁₀

47₁₀ 2₁₀

46₁₀ 23₁₀ 2₁₀

1₁₀ 22₁₀ 11₁₀ 2₁₀

1₁₀ 10₁₀ 5₁₀ 2₁₀

1₁₀ 4₁₀ 2₁₀ 2₁₀

1₁₀ 2₁₀ 1₁₀

0

47₁₀=101111

0,4₁₀

2₁₀

0,8₁₀

2₁₀

1,6₁₀

2₁₀

1,2₁₀

2₁₀

0,8₁₀

2₁₀

1,6₁₀

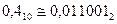
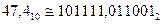
2. Преобразовать 47,4₁₀ в восьмеричную систему.

47,4₁₀=47₁₀+0,4₁₀

47₁₀ 8₁₀

40₁₀ 5₁₀ 47₁₀=57₈

7₁₀

0,4₁₀

8₁₀

3,2₁₀

8₁₀

1,6₁₀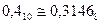

8₁₀

4,8₁₀

8₁₀

6,4₁₀

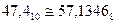
Анализ рассмотренных примеров позволяет сделать выводы:

- чем меньше основание новой системы счисления, тем больше разрядов в изображении числа;

- перевод чисел из десятичной системы в двоичную требует выполнения значительного количества действий;

- чем больше основание системы по отношению к десяти, тем менее удобно оно для человека.

Пример 3: 47,4₁₀ преобразовать в шестнадцатиричную систему.

47,4₁₀=47₁₀+0,4₁₀

47₁₀ 16₁₀

32₁₀ 2₁₀ 47₁₀=2F₁₆

15₁₀

0,4₁₀

16₁₀

6,4₁₀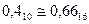

16₁₀

6,4₁₀

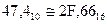
Примеры обратных переводов чисел, т.е. из системы с 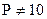в систему Q=10:

Пример 1:

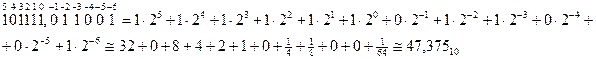
Анализ полученного результата позволяет сделать вывод, что истинное значение в новой десятичной системе счисления получить не удается, результат есть приближенное уменьшенное значение, причем количество разрядов в дробной части исходного числа определяет степень погрешности результата. Чем разрядов больше, тем погрешность меньше.

Пример 2: 2F,66₁₆ преобразовать в десятичную систему.

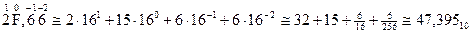
Анализ обратных преобразований подтверждает ранее сделанные выводы о количестве цифр при изображении чисел в различных традиционных системах счисления, а также количестве действий при свертывании полиномов. Исходя из изложенного были разработаны промежуточные методы перевода чисел из десятичной системы в двоичную и наоборот, с использованием промежуточных систем счисления.

Поиск по сайту: