Ітеративний метод розрахунку координатспоживача

Розглянемо застосування псевдодальномірного методу для визначення координат споживача при мінімально необхідній і надлишковій кількості видимих навігаційних супутників при використанні однієї супутникової навігаційної системи.

Псевдовіддаль до навігаційного супутника визначається, як функція:

. (2.20)

Задамося деякими апріорно відомими або заданими координатами споживача x₀, y₀, z₀, h_t0 і обчислимо псевдовіддалі до всіх видимих навігаційних супутників:

.

Позначимо векторами-стовпцями шукані координати споживача, виміряні псевдовіддалі і розрахункові псевдовіддалі відповідно:

, (2.21)

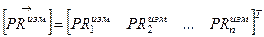, (2.22)

, (2.23)

де Т- знак транспонування матриці.

Утворимо з матриць (2.22) і (2.23) різницеву матрицю:

. (2.24)

Матрицю (2.24) запишемо з обліком (2.21)

. (2.25)

Допустимо, що матриця (2.24) дорівнює [ 0 ] або майже дорівнює [ 0 ], де [ 0 ] – нульовий вектор - стовпець.

Розкладемо матричну функцію в (2.25) у ряд Тейлора в околиці вектора :

. (2.26)

Використовуючи вираження (2.26), запишемо матричне рівняння, що поєднує виміри до n навігаційних супутників:

, (2.27)

де [G₀] – матриця похідних.

Запишемо матричне рівняння (2.27) у вигляді:

, (2.28)

і розв'язний (2.28) відносно .

Якщо кількість видимих супутників дорівнює чотирьом, то рішення матричного рівняння має вигляд:

(2.29)

де «-1»- знак зворотної матриці.

У загальному виді матричне рівняння (2.28) необхідно вирішувати при розмірності матриць, що відповідає числу спостережуваних супутників – n. У цьому випадку система рівнянь є перенадлишковою, а матриця прямокутної (має n рядків і чотири стовпці). Для приведення матриці (2.28) до форми, придатної для рішення, помножимо ліву й праву частини (2.28) на транспоновану матрицю [G₀]^T і матрицю [ W]^-1 = [P]^T´[P ], де [P] є матриця вагарень коефіцієнтів:

. (2.30)

Рішення (2.30) буде мати вигляд:

. (2.31)

Матриці в (2.31) мають наступну структуру:

; (2.32)

; (2.33)

; (2.34)

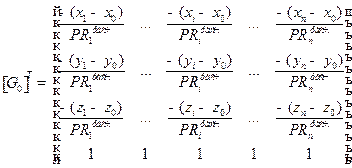; (2.35)

. (2.36)

Вираження (2.31) є перший крок методу послідовних наближень. Для визначення координат споживача даним методом необхідно задати початкове наближення вектор , необхідну точність визначення координат і погрішності h_t: d_x, d_y, d_z, d_h. При цьому вираження (2.31) записується в рекурентному вигляді:

, (2.37)

де j змінюється від 0 до K, а K+1 є число ітерацій, що змінюється доти, поки не буде виконана умова:

. (2.38)

ВЫПОЛНЕНИЕ КР

Поиск по сайту: