Векторный анализ

1. Найти производную скалярного поля 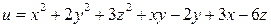в точке 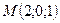по направлению вектора , где 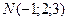, а также градиент этого поля в точке М и наибольшую скорость возрастания поля U в точке М.

2. Найти векторные линии векторного поля и изобразить три из них на координатной плоскости.

3. Найти дивергенцию и ротор векторного поля

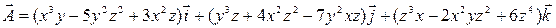
в точке М (1;0;1).

4. Вычислить поток векторного поля 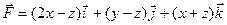через часть плоскости , вырезанную координатными плоскостями и лежащую в первом октанте в том направлении нормали, которая образует с осью 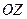острый угол.

5. Вычислить поток векторного поля через поверхность, ограниченную параболоидом 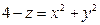и плоскостями 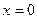, , , применяя формулу Гаусса-Остроградского.

6. Вычислить циркуляцию векторного поля 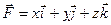вдоль замкнутого контура 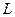, полученного при пересечении плоскости 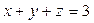с координатными плоскостями в положительном направлении, непосредственно и по формуле Стокса.

7. Вычислить циркуляцию векторного поля 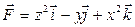по контуру 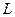, образованному при пересечении поверхности с плоскостями , , , пользуясь формулой Стокса.

8. Проверить, будет ли соленоидальным и потенциальным поле

.

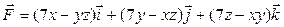В случае потенциальности поля найти его потенциал .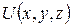

9. Доказать, что .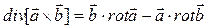

10. Доказать, что rot rot = grad div - .

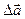Индивидуальное задание №11

Интегралы, зависящие от параметра

1. Вычислить 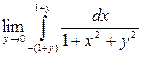. Обосновать.

2. Вычислить интеграл 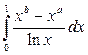, 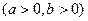. Воспользоваться теоремой об интегрируемости по параметру собственного интеграла.

Рассмотреть .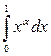

3. Найти , , 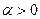дифференцируя несобственный интеграл 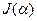по параметру 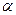. Привести обоснование.

4. С помощью критерия Коши исследовать несобственный интеграл 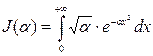на равномерную сходимость на множестве .

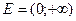5. Вычислить .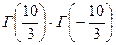

6. Вычислить .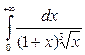

7. Доказать равенство .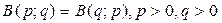

8. Найти преобразование Фурье функции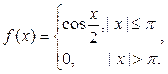

9. Найти пару синус – или косинус-преобразований Фурье функции:

.

10. Представить функцию 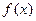интегралом Фурье, если

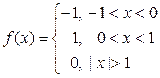
Поиск по сайту: