Определенный интеграл и его приложения

1. Вычислить определенный интеграл:

1.1. 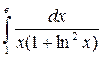; 1.2. .

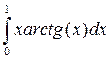2. Вычислить несобственные интегралы (или установить их расходимость):

2.1. 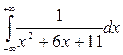; 2.2. .

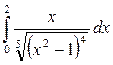3. Вычислить площадь фигуры, ограниченной линиями:

3.1. , , , ;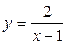

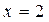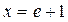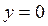3.2. 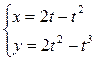, 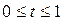; 3.3. , .

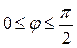4. Найти длину дуги кривой:

4.1. от точки А (0;0) до точки В (3;0);

4.2. , ();

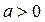4.3. .

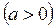5. Найти объем тела, образованного вращением вокруг оси OX (оси OY) плоской фигуры, ограниченной линиями:

5.1. , 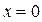; 5.2. 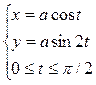; 5.3. .

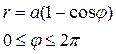6. Вычислить работу, необходимую для выкачивания масла из цилиндра высотой h=6м и радиусом основания R=2м. Удельный вес масла .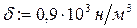

Индивидуальное задание №6

Функция нескольких переменных.

1. Найти области определения функци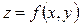й и 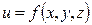. В случае 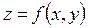изобразить область определения на координатной плоскости:

1.1. ; 1.2. .

2. Найти линии уровня функции 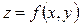(построить три из них) и поверхности уровня функции :

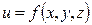2.1. 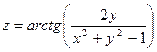; 2.2. .

3. Найти все частные производные второго порядка функции

.

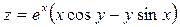4. Проверить, удовлетворяет ли функция 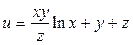заданному уравнению:

.

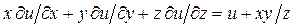5. Найти дифференциал второго порядка функции 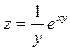в точке А(0; 1).

6. Заданы функция и две точки А(1; 2) и В(1,03; 1,98). Требуется:

а) вычислить приближенное значение функции 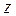в точке В;

б) линеаризовать функцию 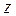в окрестности точки А.

7. Для функции 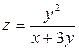найти:

а) производную по направлению вектора 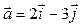в точке М₀(1; 3);

б) градиент и наибольшую скорость изменения функции в точке М₀(1; 3).

8. Найти частные производные первого порядка функции 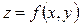, заданной неявно уравнением: .

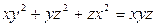9. Составить уравнения касательной плоскости и нормали к поверхности:

9.1. в точке А ;

9.2. 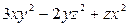в точке В .

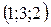10. Найти экстремумы функции .

Индивидуальное задание №7

Числовые ряды.

1. Исследовать на сходимость следующие ряды:

1.1. 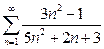; 1.2. , ;

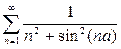1.3. ; 1.4. ;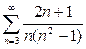

1.5. 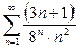; 1.6. ;

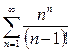1.7. 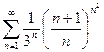; 1.8. ;

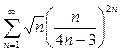1.9. ; 1.10. .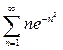

2. Выяснить, какие из данных знакочередующихся рядов сходятся абсолютно, какие условно, какие расходятся:

2.1. ; 2.2. ;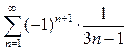

2.3. 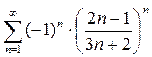; 2.4. ;

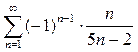2.5. 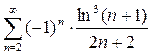; 2.6. ;

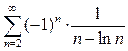2.7. 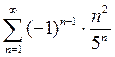; 2.8. .

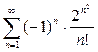3. Исследовать ряды на сходимость. В случае сходимости найти сумму ряда:

3.1. 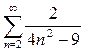; 3.2. .

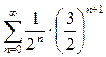Индивидуальное задание №8

Поиск по сайту: