АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Функция Лапласа

Читайте также:
  1. Exercises for Lesson 4. There is / there are. Функция. Формы. Использование в ситуации гостиницы
  2. II. Вторая стадия. Функция производительного капитала
  3. Автокорреляционная функция. Коррелограмма
  4. Автокорреляция остатков модели регрессии. Последствия автокорреляции. Автокорреляционная функция
  5. Анатомия и методы исследования глотки. Лимфаденоидное глоточное кольцо Вальдеера - Пирогова. Какие лимфообразования входят в лимфоэпителиальный барьер, его функция.
  6. Башмаки Лапласа
  7. Болжау функциясы.
  8. В четвертых, функция обеспечивается общественной поддержкой и властной силой государства.
  9. Вопрос 10: Функция вестибулярного анализатора. Адекватные раздражители вестибулярного анализатора. Законы лабиринтологии.
  10. Воспроизводящая функция представляется аппроксимирующим полиномом
  11. Глава II. РЕФЛЕКТОРНО-ДВИГАТЕЛЬНАЯ ФУНКЦИЯ, ПЕРИФЕРИЧЕСКИЕ И ЦЕНТРАЛЬНЫЕ ПАРАЛИЧИ
  12. ГОЛОСООБРАЗОВАТЕЛЬНАЯ ФУНКЦИЯ ГОРТАНИ

 

Интегральная теорема Муавра—Лапласа

Пусть 0< p <1, тогда для схемы Бернулли при n® ¥ для любых a и b справедлива формула .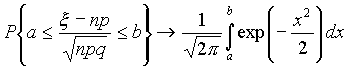

Это означает, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k 1 и k 2, можно использовать формулу , где 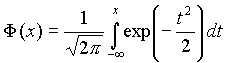— функция Лапласа, , .

Точность этой приближенной формулы растет с ростом n.

 

12. Дискретные и не прерывные случайные величины, их числовые характеристики.

 

 

Случайная величина 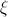называется дискретной случайной величиной, если она принимает не более чем счетное число значений. Задание дискретной случайной величины по определению равносильно заданию закона распределения случайной величины в следующем виде:


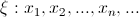
где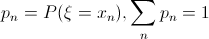

Пример. дискретная случайная величина Бернулли(закон распределения Бернулли). Закон распределения дискретной случайной величины Бернулли имеет следующий вид: 0<p<1

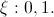
Такому распределению соответствует бросание монеты, на одной стороне которой - 0, а на второй - 1.

 

Распределение случайной величины 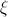называется непрерывным, а сама случайная величина - непрерывной случайной величиной, если для любого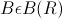

,

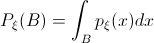где 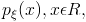- интегрируемая по Лебегу функция. Функция называется плотностью распределения случайной величины .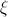

Теорема 1: Для того чтобы случайная величина 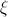была непрерывной случайной величиной, необходимо и достаточно, чтобы для любого

Пример. нормальная непрерывная случайная величина, или непрерывная случайная величина Гаусса(нормальное распределение). Непрерывная случайная величина 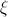имеет нормальное (гауссовское) распределение, если её плотность распределения имеет вид

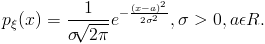
Если 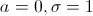, то распределение называется стандартным нормальным распределением.

 

13. Статически зависимые и не зависимые случайные величины. Примеры.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)