Классическое определение вероятности

Вероятность события численно характеризует степень возможности его появления в рассматриваемом опыте.

Пусть производится опыт с n равнозначными исходами, образующими полную группу несовместных событий. Такие исходы называются элементарными исходами (событиями), случаями, шансами. Случай, который приводит к наступлению события А, называется благоприятным (или благоприятствующим) ему.

Вероятностью события А называется отношение числа m случаев, благоприятствующих этому событию, к общему числу n случаев.

p(A)=m/n

Такое определение вероятности называется классическим определение вероятности.

Из классического определения следуют свойства вероятности:

· 0≤p(A)≤1

· p(Ø)=0,

· p(Ω)=1,

· p(Ā)=1-p(A)

· p(A+B)= p(A)+ p(B), если AB=Ø

Геометрическое определение вероятности

Обобщением понятия "классической вероятности" на случай опытов с бесконечным (вообще говоря, несчетным) числом исходов является понятие "геометрической вероятности". К этому понятию приводят задачи на подсчет вероятности попадания точки в некую область (отрезок, часть плоскости, часть тела и т.д.).

Пусть пространство элементарных событий Ω представляет собой некоторую область плоскости. Тогда в качестве событий могут рассматриваться области А, содержащиеся в Ω.

Вероятность попадания в область А точки, наудачу выбранной из области Ω, называется геометрической вероятностью события А и находится по формуле:

p(A)=S(Ω)/S(Ω),

где S(A) и S(Ω) площади областей А и Ω соответственно.

Случай, когда Ω представляет собой отрезок или трехмерную область, рассматривается аналогично.

4. Действия над событиями. Алгебра Буля.

Действия над случайными событиями и отношения между ними определяются по аналогии с действиями и отношениями в теории множеств.

Обозначаем 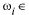А, если 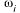— элементарный исход события А; А 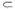В, если событие А влечет за собой В; А, В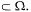

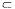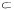Равенство (эквивалентность) событий: А = В, если А В и В А.

О: Суммой 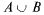событий A и В называется их теоретико-множественное объединение, т.е. событие, состоящее из элементарных событий 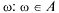или В.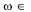

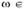Произведением АВ (А В) событий А и В называется их теоретико-множественное пересечение, т.е. событие, состоящее из элементарных событий: А и 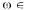В. Разностью 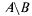событий Аи В называется их теоретико-множественная разность, т.е. событие, состоящее из элементарных событий 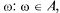но 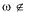В. Противоположным событием 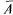для события A 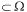называется теоретико-множественное дополнение А до т.е. происходит тогда, когда А не происходит.

Примеры:

1. А— выигрыш по займу 1; В — выигрыш по займу 2. Тогда А В — выигрыш хотя бы по одному из займов (в частности, сразу по двум).

2. А — прохождение I тура на конкурсе, В — прохождение II тура. Тогда АВ — успешное прохождение I и II туров.

3. Бросают монету. А — выпадение герба, 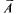— выпадение решки.

Множество случайных событий А и образуют булеву алгебру — алгебру событий, связанных с заданным экспериментом.

О: События А и В называются несовместными, если наступление А исключает наступление В, т.е. АВ= В этом случае используют А В = А+ В.

Таким образом А, 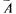— несовместные события.

О: Множество (система) событий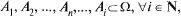

называется полной группой событий S, если

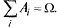
5. Теорема для сложения вероятностей для совместных событий. Теорема для сложения вероятностей не совместных событий.

Теорема. Вероятность суммы 2-х совместных событий равна сумме вероятностей этих событий без учета их совместного появления. p (A + B)= p (A)+ p (B)− p (AB)

Доказательство:

A + B = AB + AB + AB (сумма несовместных пар)

Тогда p (A + B)= p (AB)+ p (AB)+ p (AB)

Событие A = AB + AB,

Событие B = AB + AB

p (A + B)= p (A)− p (AB)+ p (B)− p (AB)+ p (AB)= p (A)+ p (B)− p (AB)

Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р (А + В) = Р (А) + Р (В).

Введем обозначения: n — общее число возможных элементарных исходов испытания; m₁ — число исходов, благоприятствующих событию A; m₂— число исходов, благоприятствующих событию В.

Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m₁ + m₂. Следовательно,

Р (A + В) = (m₁ + m₂) / n = m₁ / n + m₂ / n.

Приняв во внимание, что m₁ / n = Р (А) и m₂ / n = Р (В), окончательно получим

Р (А + В) = Р (А) + Р (В).

6. Условная вероятность. Пример. Теорема умножения вероятностей для зависимых событий. Независимые события. Теорема умножения для независимых величин.

Поиск по сайту: