 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теорема Чебышева
Теорема. Если Х1, Х2, …, Хn- попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное числоe, вероятность неравенства
будет сколь угодно близка к единице, если число случайных величин достаточно велико.
Т.е. можно записать:
Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:
Дробь, входящая в записанное выше выражение есть не что иное как среднее арифметическое возможных значений случайной величины.
Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.
Отклоняясь от математического ожидания как в положительную так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.
Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.
23. Следствие из теоремы Чебышева.
Если дисперсии независимых случайных величин ограничены одной и той же постоянной С, то, как бы мало не было данное положительное число Е, вероятность того, что отклонение средней арифметической этих случайных величин от средней арифметической их математических ожиданий а1, а2, …, аn не превзойдет по абсолютной величине Е, как угодно близка к единице, если число случайных величин достаточно велико.
Следствие.
Если независимые случайные величины имеют одинаковые, равные a, математические ожидания, дисперсии их ограничены одной и той же постоянной С, а число случайных величин достаточно велико, то, сколько мало ни было данное положительное число Е, как угодно близка к единице вероятность того, что отклонение средней арифметической этих случайных величин от а не превзойдет по абсолютной величине Е.
При доказательстве теоремы Чебышева и следствия из нее с помощью неравенства Чебышева получаем такие оценки:
 , (63)
, (63)

24. Закон больших чисел в форме Бернулли.
(ЗБЧ Бернулли). Пусть событие  может произойти в любом из
может произойти в любом из  независимых испытаний с одной и той же вероятностью
независимых испытаний с одной и той же вероятностью  , и пусть
, и пусть  — число осуществлений события
— число осуществлений события  в
в  испытаниях. Тогда
испытаниях. Тогда  . При этом для любого
. При этом для любого 
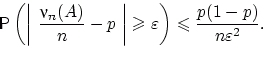
Доказательство. Заметим, что  есть сумма независимых, одинаково распределённых случайных величин, имеющих распределение Бернулли с параметром
есть сумма независимых, одинаково распределённых случайных величин, имеющих распределение Бернулли с параметром  (индикаторовтого, что в соответствующем испытании произошло
(индикаторовтого, что в соответствующем испытании произошло  ):
):  , где
, где

и  ,
, 
Осталось воспользоваться ЗБЧ в форме Чебышёва и неравенством  .
.
25. Случайные векторы. Совместный закон распределения двух случайных величин.
Горох!)))
26. Закон распределения дискретной случайной точки.
Поиск по сайту: