 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Условная вероятность
Пример Игральная кость подбрасывается один раз. Известно, что выпало более трёх очков. Какова вероятность того, что выпало чётное число очков?
Зная, что выпало более трёх очков, мы можем сузить множество всех возможных элементарных исходов до трёх одинаково вероятных исходов: 
, из которых событию 
благоприятствуют ровно два: 
. Поэтому 
.
Посмотрим на вопрос с точки зрения первоначального эксперимента. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: 
. Слова «известно, что выпало более трёх очков» означают, что в эксперименте произошло событие 
. Слова «какова при этом вероятность того, что выпало чётное число очков?» означают, что нас интересует, в какой доле случаев при осуществлении 
происходит и 
. Вероятность события , вычисленную в предположении, что о результате эксперимента уже что-то известно (событие произошло), мы будем обозначать через 
.
Мы хотим найти, какую часть составляют исходы, благоприятствующие внутри (т.е. одновременно и ), среди исходов, благоприятствующих .
Мы пришли к выражению, которое можно считать определением условной вероятности.
УМНОЖЕНИЕ ВЕРОЯТНОСТЕЙ ЗАВИСИМЫХ СОБЫТИЙ
Теорема. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них наусловную вероятность другого, вычисленную в предположении, что первое событие уже наступило: P (AB)= P (A) P (A | B). Вероятность совместного появления трех зависимых событий: P (ABC)= P (A) P (A | B) P (AB | C).
Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
. Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.
Решение.
Пусть А – попадание первого стрелка, 
;
В – попадание второго стрелка, 
.
Тогда 
- промах первого, 
;
- промах второго, 
.
Найдем нужные вероятности.
а) АВ – двойное попадание, 
б) – двойной промах, 
.
в) А + В – хотя бы одно попадание,
.
г) 
– одно попадание, 
7. Формула полной вероятности.
Пусть событие А может произойти только совместно с одним из событий Н 1, Н 2,…, Нп, образующих полную группу несовместных событий. Тогда события Н 1, Н 2,…, Нп называются гипотезами .
Теорема. Вероятность события А, наступающего совместно с гипотезами Н 1, Н 2,…, Нп, равна: 
где P (Hi) – вероятность i той гипотезы, а P (A/Hi) – вероятность события А при условии реализации этой гипотезы. Формула носит название формулы полной вероятности.
Доказательство.
Можно считать событие А суммой попарно несовместных событий АН 1, АН 2,…, АНп. Тогда из теорем сложения и умножения следует, что 
что и требовалось доказать.
8. Формула Байеса.
Пусть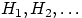 
— полная группа событий, и — некоторое событие, вероятность которого положительна. Тогда условная вероятность того, что имело место событие 
, если в результате эксперимента наблюдалось событие , может быть вычислена по формуле:
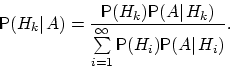
Доказательство. По определению условной вероятности,
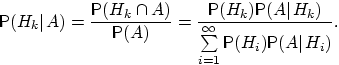
9. Сводка основных правил теории вероятности.
10. Схема с повторением независимых испытаний (схема Бернулли). Формула Бернулли.
Испытания независимы, если вероятность элементарных исходов не зависят от предыдущих испытаний.
– число независимых испытаний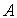 
– может произойти с вероятностью 
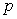С какой вероятностью событие 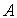произойдет 
раз
, где 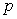– вероятность успеха 
– вероятность неуспеха 
– число сочетаний способов
Доказательство: 
Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность 
того, что событие A наступит k раз в n независимых испытаниях, равна: 
, где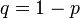 
.
[править]Доказательство
Так как в результате 
независимых испытаний, проведенных в одинаковых условиях, событие 
наступает с вероятностью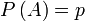 
, следовательно противоположное ему событие с вероятностью 
.
Обозначим 
— наступление события в испытании с номером 
. Так как условия проведения опытов одинаковые, то эти вероятности равны. Пусть в результате опытов событие наступает 
раз, тогда остальные 
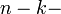раз это событие не наступает. Событие может появиться раз в испытаниях в различных комбинациях, число которых равноколичеству сочетаний из элементов по . Это количество сочетаний находится по формуле:
.
При этом вероятность каждой комбинации равна произведению вероятностей:
.
Применяя теорему сложения вероятностей несовместных событий, получим окончательную Формулу Бернулли:
, где .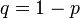
11. Теорема Пуассона. Функция Лапласа. Интегральная формула Муавра-Лапласа.
Теорема Пуассона.Пусть есть 
Пусть также дана последовательность 
такая, что
Тогда
Поиск по сайту: