Закон и функция распределения дискретной случайной величины

Пусть 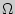= { } - дискретное (конечное или счетное) пространство элементарных событий.

Случайной величиной 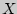называется функция 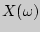, определенная на множестве 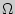и принимающая вещественные (комплексные) значения.

Если 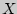- случайная величина, а , ,...- ее значения, то совокупность всех элементарных событий, на которых 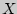принимает фиксированное значение , образует событие

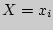{ } = , т.е.

Обозначим через 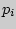вероятность этого события:

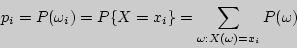
(знак суммы означает, что сумма берется по таким, для которых X( =x .

Функция 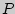{ 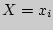} = 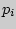( =1, 2,...) называется законом распределения (вероятностей) дискретной случайной величины (д.с.в.) .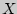

Учитывая, что при экспериментах фиксируются значения случайной величины 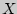, закон распределения д.с.в. даем в виде таблицы

X			...		...
			...		...

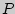
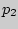
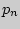
где в верхней строчке написаны значения случайной величины, а в нижней - под каждым - вероятности { 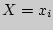}. Заметим, что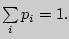

27. Закон распределения непрерывной случайной точки.

28. Совместная плотность вероятностей пары случайных величин. Свойства. Необходимое и достаточное условие независимости случайных величин.

x₁,x₂,...,x_n (плотность вероятности совместного распределения):

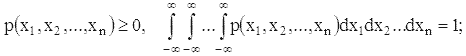
и для любых a_i < b_i, i = 1, 2,..., n, вероятность одновременного выполнения неравенств a₁ < x₁ < b₁,a₂ < x₂ < b₂,...,a_n < x_n < b_n равна

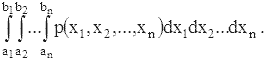
Если существует совместная плотность случайных величин x₁, x₂,..., x_n, то для независимости этих величин необходимо и достаточно, чтобы совместная плотность была произведением плотностей отдельных величин, т.е.
p(x₁, x₂,..., x_n) = p₁(x₁) • p₂(x₂) •... • p_n(x_n),
где p_i - плотность вероятности случайной величины x_i. По совместной плотности вероятности случайных величин можно найти распределение вероятностей любых функций от этих величин. Так, например, для двух независимых случайных величин с плотностью распределения p₁(x) и p₂(x) плотность распределения их суммы задается формулой свертки:

29. Совместный закон распределения двух случайных величин. Числовые характеристики.

30. Ковариация двух случайных величин. Коэфицент коррелиации.

Пусть 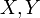— две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда их ковариация определяется следующим образом:

,

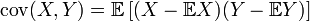в предположении, что все математические ожидания в правой части определены.

Рассмотрим две дискретные случайные величины: Х и У. Пусть их возможные значения соответственно равны:

х₁, х_2, х₃,… х_i, … x_s

y₁, y₂, y_3,… y_j, … y_r

Среднее значение первой величины составляет х и второй - у. Введем в рассмотрение отклонения воз­можных значений случайных величин от их средних зна­чений, которые будем

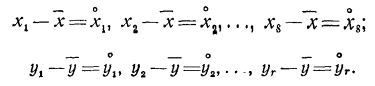
коротко обозначать следующим образом:

В свое время (см. §6 гл. 3) говорилось, что среди отклонений имеются числа как положительные, так и отрицательные. Вероятности отклонений равны вероятностям

соответствующих значений случайных величин, т. е.

o o

P(x_i -x) =P(х_i)=P(х_i) и Р(у_j - у) =Р(у_j)=Р(у_i )

Если средние значения у случайных величин X или Y равны нулю, то их отклонения x_i и y_j равны соответствующим значениям случайных величин.

Положим далее, что известны условные и безусловные законы распределения случайных величин Х и Y и закон распределения системы этих дискретных величин Р(x_i,y_j).

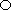Перемножим все возможные отклонения одной случайной величины x_i почленно на все возможные отклонения друтой y_j с учетом их вероятностей и все произведения сложим. В итоге получим величину, которая в виде общей формулы может быть записана следующим

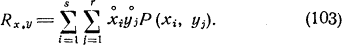
образом:

Индексы суммирования i, j указывают, что в сумму должны быть включены все возможные

о о

сочетания значений x_i и y_j.

о о

Величина R_x,y представляет собой среднее значеи е произведений x_i на y_j и называется в теории вероятностей корреляционным моментом.

Коэффициентом корреляции между двумя случайными величинами, или, иначе, нормированным корреляционным моментом, называется отношение корреляционного момента R_xy к произведению среднеквадратических отклонений случайных величин s_х и s_y:

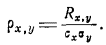
31. Операционное исчисление. Определение оригинала и L-изображения (преобразования Лапласа).

Определение. Будем называть функцией-оригиналом действительнозначную или комплекснозначную функцию f (t) действительной переменной t, удовлетворяющую условиям:
1. f (t) = 0 при t < 0;
2. Существуют такие постоянные M > 0 и σ₀ ≥ 0, что | f (t) | ≤ M · e ^σ₀ ^t;
3. На любом отрезке [ a, b ] (0 ≤ a < b < ∞) функция удовлетворяет условиям Дирихле (т.е. непрерывна или имеет конечное число устранимых разрывов и разрывов первого рода; монотонна или имеет конечное число экстремумов).
Смысл этих условий такой.
1. Так как одно из основных приложений операционного исчисления - решение задач с начальными условиями (задач Коши), то поведение функций до начального момента t = 0 несущественно;
2. Параметр σ₀ во втором условии принято называть показателем роста функции f (t). Само второе условие означает, что скорость роста функции-оригинала не может быть больше экспоненциальной. В совокупности с третьим условием это обеспечивает существование и определенные полезные свойства функции-изображения и не является обременительным.

Определение. Изображением по Лапласу функции-оригинала f (t) (или преобразованием Лапласа функции f (t)) называется функция комплексной переменной p, определяемая равенством
.
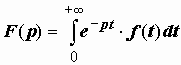Интеграл в правой части этого определения сходится абсолютно в любой точке p, удовлетворяющей неравенству Re p ≥ σ₁, где σ₁ - произвольной число, такое, что σ₁ > σ₀. Действительно, 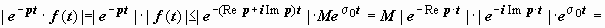(так как | e ^{− i Im p · t} | = | cos(Im p · t) − i sin(Im p · t)| = 1) = M | e ^{−Re p · t} |· e ^·σ₀ ^t = M e ^{−(Re p − σ}₀^{) t} ≤ M e ^−(σ₁ ^{− σ}₀^{) t} , а интеграл 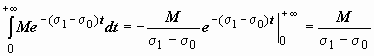сходится. Таким образом, мы доказали, что изображение F (p) определено в любой точке p, такой что Re p > σ₀, т.е. в полуплоскости справа от прямой Re p = σ₀. Как следствие, показатель скорости роста оригинала число σ₀ часто называют абсциссой сходимости.
Заметим, что мы доказали также, что 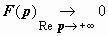: так как | e ^{− pt} · f (t)| ≤ M e ^{−(Re p − σ}₀^{) t} , то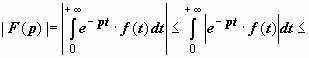 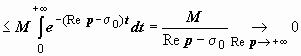. Кроме того, в оценке | e ^{− pt} · f (t)| ≤ M e ^−(σ₁ ^{− σ}₀^{) t} мы мажорировали модуль подынтегральной функции функцией, не зависящей от p, интеграл от которой сходится. Как и в теории функциональных рядов, этого достаточно, чтобы сходимость интеграла была равномерной по переменной p, поэтому функцию F (p) можно дифференцировать и интегрировать по этой переменной.

32. Основные свойства L-изображений.

Свойства изображений

§ Линейность

Изображение линейной комбинации функций равно линейной комбинации изображений с теми же коэффициентами.

где a и b – произвольные комплексные числа.

§ Теорема подобия

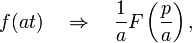
где a>0.

§ Дифференцирование оригинала

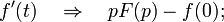
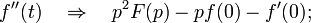
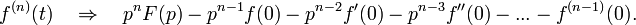
§ Дифференцирование изображения

§ Интегрирование оригинала

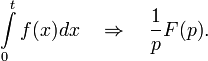
§ Интегрирование изображения

§ Теорема смещения

§ Теорема запаздывания

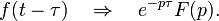
§ Теорема умножения (свёртки)

33. Таблица L-изображений.

№	f(t)	F(p)	№	f(t)	F(p)

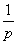
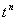
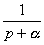
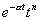
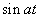
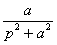
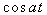
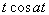
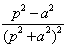
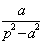
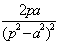
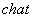
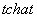
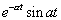
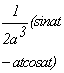
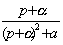
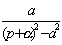
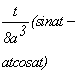
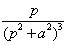
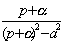
34. Восстановление оригинала по его L-изображению. Формула обращения.

Пример. Восстановить оригинал по изображению:

а) ; б) .

Решение. а) по табл. 2 находим 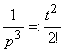и 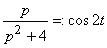. По табл. 1 учитываем запаздывание аргумента оригинала, а именно и

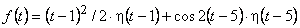. Окончательно получаем оригинал , или

б) аналогично имеем последовательно , .

35. Применение операционного исчисления к решению ЛДУ и систем ЛДУ.

Поиск по сайту: