КВАНТОВАНИЕ СООБЩЕНИЙ ПО УРОВНЮ

Квантованием по уровню называют дискретизацию множества значений непрерывного сигнала по уровню, то есть по амплитуде параметра. Идея квантования по уровню заключается в следующем. Весь диапазон возможных изменений сигнала (функции) разбивается на N различимых величин – уровней квантования. В результате квантования сигнала каждое из его значений данного интервала округляется до некоторого уровня. Порогами квантования называются величины, при сравнении с которыми исходного непрерывного сигнала в процессе квантования определяется его принадлежность к уровню квантования. Величина, представляющая собой разность между двумя соседними уровнями, называется шагом квантования. Замена исходных значений функции соответствующими дискретными значениями – уровнями квантования – вносит ошибку квантования, называемую шумом квантования.

Существует три способа квантования:

1-й способ квантования - путем соотнесения исходного значения сигнала с ближайшим значением уровня. Информационная система содержит устройство квантования, которое выполняет операцию квантования непрерывного сигнала по уровню. В процессе такой операции отдельное значение исходного непрерывного сигнала соотносится с одним из возможных значений уровней; если исходное значение оказывается в пределах двух соседних порогов квантования, то это значение заменяется уровнем квантования, заключенным между данными порогами. В этом случае квантование происходит по методу соотнесения с ближайшим значением уровня. Этот способ квантования аналогичен округлению чисел до ближайшего целого. При таком способе вместо исходного непрерывного сигнала мы получим квантованный сигнал, представленный временной диаграммой на рис.1.5.

f(t) - исходный непрерывный сигнал;

f ^*(t) - квантованный сигнал;

f_i, f_i+1,... - значения соседних порогов квантования (пунктир);

D f_i - шаг квантования, D f_i = f_i+1 - f_i;

- значения уровней квантования (сплошные линии).

Таким образом, очевидно, что в процессе квантования неизбежно возникает принципиальная или методическая ошибка квантования - шум квантования; ее величина для момента времени t определяется в виде

Для этого способа ошибка квантования не превышает половины шага квантования

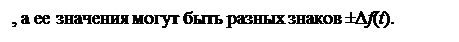
2-й способ квантования - путем соотнесения исходного значения с ближайшим ²снизу² значением уровня. В этом случае i -е пороговое значение совпадает со значением (i +1)-го уровня. Данный способ аналогичен округлению числа до ближайшего целого снизу. Соответствующая временная диаграмма представлена на рис.1.6.

Ошибка квантования всегда положительна (D f(t) > 0) и не превышает величинушага квантования ( ¦).

3-й способ квантования - путем соотнесения исходного значения с ближайшим ²сверху² значением уровня. Пороги и уровни совпадают по номерам и значениям. Шум квантования всегда отрицательный (D f(t)< 0) и не превышает величину шага квантования (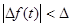 ¦_i). Этот способ аналогичен округлению числа до ближайшего целого сверху.

Соответствующая временная диаграмма представлена на рис.1.7.

Равномерным квантованием называется такое квантование, при котором шаг квантования есть постоянная величина. В большинстве случаев применяется равномерное квантование.

Шаг квантования выбирается исходя из необходимой точности передачи сигнала. Если же при этом существуют внешние помехи, то необходимо, чтобы амплитуда помех не превышала половины шага квантования, тогда возможно будет восстановить заданный уровень, так как воздействие помехи не выведет значение сообщения за зону, соответствующую данному уровню квантования. Кроме уровней выделяют пороги квантования. При равномерном квантовании расстояние между двумя соседними порогами равняется шагу квантования.

Из трех способов квантования первый дает минимальную среднюю ошибку квантования при одном и том же шаге квантования, поэтому на практике часто используется именно этот способ.

Для более точного отображения исходного сигнала необходимо увеличивать число уровней, т. е. уменьшать шаг квантования (рис. 1.8-1.9).

Однако бесконечное уменьшение шага квантования физически невозможно, а формально не имеет смысла, так как мы опять возвращаемся к непрерывному сигналу. Уменьшать шаг до бесконечности невозможно также из-за влияния помех. Сообщения по мере передачи по каналам связи или по мере хранения в памяти искажаются под воздействием помех, поэтому на приемной стороне или при считывании сигнала должен находиться еще один квантователь. Этот квантователь, как и исходный квантователь сигналов, для опознавания сигнала должен соотносить реальный сигнал с возможными значениями уровней. Для некоторых значений это соответствие может быть неправильным и на приемной стороне могут быть ложные восприятия соседних уровней. Таким образом, исходный сигнал, поступающий от источника непрерывных сигналов, в системе квантования по уровню искажается из-за самого квантования и, кроме того, под воздействием помех, как показано на рис.1.10.

Временные диаграммы:

Увеличение шага квантования в системе квантования, при неизменном уровне помех, приводит к подавлению помех, поэтому с амый простой способ защиты квантованного сигнала от помех - увеличение шага квантования. Однако при этом мы увеличиваем шум квантования, т.е. вносим погрешность за счет грубого квантования.

Различают следующие две модели помех (два типа помех):

a) аддитивные помехи формируют смесь сигнала с помехой путем алгебраического суммирования их амплитуд:

fсп(t)= f*(t) ± fп(t), где f_n(t) - амплитуда помехи;

б) мультипликативные помехи формируют смесь сигнала с помехой путем перемножения их значений:

fсп(t)=k · f*(t) · fп(t), где k - масштабный коэффициент.

(При имитации работы системы квантования на лабораторных работах моделируются аддитивные помехи.)

Кроме равномерного квантования, в некоторых случаях используют неравномерное квантование, при котором шаг квантования ∆f_i - переменная величина в зависимости от номера уровня: ∆f_i = f_i+1 - f_i. В некоторых диапазонах изменения сигнала, для уточнения его значений, шаг квантования делают меньше.

Такая система применяется тогда, когда возникает необходимость отображать значения сигнала в некоторых диапазонах точнее, чем за их пределами, как это показано на рис.1.11.

При построении устройства для равномерного квантования необходимо:

1) определить диапазон изменения сигнала;

2) определить шаг квантования.

При определении шага квантования следует учитывать:

- желаемую точность отображения сигнала;

- влияние помех, величина которых ставит ограничения на минимальную величину шага квантования.

При равномерном квантовании число уровней квантования определяется диапазоном изменения сигнала и величиной шага квантования в виде:

n_max= (f_max - f_min) / ∆f, где f_max, f_min – максимальное и минимальное возможные значения сигнала в данной информационной системе.

Если известен характер изменения помех, то минимальную величину шага квантования можно определить численно. При моделировании часто имитируется случайная помеха с нормальным (гауссовым) распределением, закон которого характеризуется двумя параметрами m и б, где m - математическое ожидание (величина постоянной составляющей помехи); б - среднеквадратическое отклонение - СКО (интенсивность случайной составляющей помехи).

Изображенная на рис. 1.12. гауссова помеха имеет постоянную составляющую со знаком ²+². Обычно в системах передачи данных помеха бывает именно нормально распределенной с нулевым математическим ожиданием. Помеха может быть рассеяна более или менее сильно, но площадь под кривой распределения должна быть одинаковой и соответствовать вероятности достоверного события - единице. Степень рассеивания случайной величины (помехи) определяется значением среднеквадратического отклонения б.

При наложении такой помехи на квантованный сигнал последний становится случайной величиной f_сп(t) с математическим ожиданием, равным его уровню

(m = ), и среднеквадратическим отклонением помехи (б = б_n), как показано на рис.1.13.

Рис.1.13. Плотность распределения смеси f_сп квантованного сигнала с гауссовой помехой: _ __ __

f_i , f_i-1 , f_i+1 - данный, нижний и верхний соседние уровни квантования;

f_i , f_i+1 - соседние пороги квантования

Площади под кривой распределения за пределами пороговых значений f_i и f_i+1 данного уровня составляют вероятность искажения квантованного сигнала (ВИКС). Предположим, что допустимая ВИКС = 0,01 и нам нужно определить шаг квантования. Если известен закон распределения или характер помехи и его параметры, то можно решить обратную задачу - определить значения порогов квантования. Таким образом, шаг квантования подбирается с учетом помех двумя разными способами:

- экспериментально (или методом подбора);

- численно, аналитически, если известен характер помех.

Итак, система квантования должна содержать один квантователь на выходе источника непрерывных сигналов, а другой - на входе приемника сигналов; между ними располагается канал связи, где на передаваемый сигнал воздействуют помехи.

(В составе лабораторного программного пакета функцию источника непрерывного сигнала и функцию квантователя имитируют специальные подпрограммы. Подпрограмма источника формирует сразу весь массив значений, а подпрограмма-квантователь обрабатывает сигнал поэлементно. События в канале связи имитируются не полностью - квантованный сигнал деформируется только помехами. Помехи аддитивные, случайные и нормально распределенные).

Эффективность работы системы квантования определяется степенью искажения формы исходного сигнала. Если передается не непрерывный сигнал, а сразу квантованный или дискретный, то эффективность работы системы может определяться также частотой правильной передачи отсчетных сообщений.

Целью квантования по уровню является замена бесконечного множества непрерывных сообщений (значений параметра) конечным множеством дискретных значений. При этом становится возможным кодирование конечного множества дискретных сообщений, которое осуществляется кодовыми словами на основе алфавита меньшего объема. Значительным преимуществом системы квантования по уровню является возможность применения ее на протяженных линиях связи с промежуточными приемными пунктами. В этом случае применение такой системы позволяет избежать накопления помехи в процессе передачи сигнала по участкам, так как на каждом промежуточном пункте производится приведение сигнала к первоначальному квантованному уровню. В результате этого единственная помеха, которая остается в сигнале к моменту его прихода на конечный пункт - это шум квантования, который принципиально не устраним. Квантование сообщений позволяет обеспечить их длительное хранение без искажений в аналоговых запоминающих устройствах путем периодического считывания, квантования и записи данного сообщения на прежнее место с помощью одного и того же блока квантования.

Контрольные вопросы к пп. 1.1. и 1.2

1. Цель и суть любой дискретизации.

2. Представление сигналов функциями; понятие квантованного по уровню сигнала.

3. Цель и суть квантования сообщений по уровню; функции АЦП.

4. Определения неравномерного и равномерного квантования, уровней, порогов, шага и шума квантования.

5. Три способа квантования и соответствующая им величина шума квантования.

6. Структуры систем передачи сообщений:

· системы, передающей непрерывный сигнал квантованными сообщениями;

· системы, передающей квантованные сообщения;

· системы, передающей дискретные сообщения в форме квантованных по уровню сигналов.

7. От чего зависит и как оценивается эффективность работы этих систем?

8. Типы (модели) помех.

9. Влияние помех на квантованный по уровню сигнал.

10. Какие факторы определяют величину шага квантования для каждой системы; каково влияние этих факторов?

11. Чем ограничено минимальное значение ошибки восстановления сигнала?

Поиск по сайту: