 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Определение проверочных равенств
Проверочное равенство представляет собой одно из преобразованных уравнений алгоритма кодирования. Пусть уравнение, с помощью которого формируется содержимое некоторого избыточного разряда, включает в себя в качестве известных величин содержимое определенных информационных разрядов, которые суммируются по модулю 2. В таком случае проверка дешифратором каждого из этих уравнений сводится к проверке на четность.
Если проверка дешифратором уравнения, определяющего данный избыточный разряд, показала нарушение принятого условия (четности), то соответствующий разряд опознавателя окажется равным 1. Просмотр во второй колонке таблицы содержимого данного разряда всех опознавателей ошибок позволяет выделить номера разрядов помехоустойчивого кодового слова, в которых возможно искажение. Для разрабатываемого кода разряды опознавателя определяются следующими группами разрядов помехоустойчивого кодового слова:
1 - й (младший) - а1 È а3 È а6 È а7;
2 - й - а2 È а5 È а6 È а7;
3 - й - а1 È а2 È а4 È а7
(здесь знак È соответствует логическому “или”).
При отсутствии однократных ошибок в слове дешифратор вычислит ²нулевой опознаватель² (состоящий из одних нулей - 000). Поэтому можно записать ²проверочные равенства² дешифратора в виде следующей системы уравнений:
|
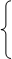a1 Å a3 Å a6 Å a7 = 0
a2 Å a5 Å a6 Å a7 = 0
a1 Å a2 Å a4 Å a7 = 0
При построении группового кода исправляющего, кроме однократных, ошибки большей кратности, необходимо учитывать следующее:
- опознаватели всех подлежащих исправлению векторов ошибок должны быть разными;
- число разрядов опознавателя ошибки должно быть по возможности меньшим, чтобы уменьшить избыточность кода;
- опознаватели векторов ошибок с единицами в нескольких разрядах устанавливаются как суммы по модулю 2 опознавателей однократных ошибок в этих разрядах, поэтому для определения правил построения кода и составления проверочных равенств достаточно правильно подобрать только опознаватели однократных ошибок в каждом из разрядов;
- выбирая в качестве опознавателей однократных ошибок в i -м разряде двоичную комбинацию с числом разрядов меньшим i, необходимо убедиться в том, что для всех остальных подлежащих исправлению векторов ошибок, имеющих единицы в i -м и более младших разрядах, получаются опознаватели, отличные от уже использованных.
В табл. 2.3 приведены опознаватели одиночных ошибок для кодов, исправляющих однократные и двукратные независимые ошибки вплоть до 15 разряда [1].
|
Поиск по сайту: