Расход. Уравнение расхода

Расход — это количество жидкости, которое протекает через данное сечение в единицу времени. Количество жидкости можно измерять в единицах объема, массы или веса. Поэтому различают объемный Q (м³/с), массовый Q_m (кг/с) и весовой Q_G (Н/с) рас­ходы. Между этими расходами существует такая же связь, как между объемом, массой и весом, т.е.

Q_m = Qр; Q_G=Qmg; Q_G= 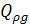(3.1)

При расчете гидравлически систем наибольшее распространение получил объемный расход Q. Очевидно, что расход связан со скоростью движения жидкости Рассмотрим эту связь применительно к параллельно струйном; течению идеальной жидкости, изображенной на рис. (3.2, а.) В иде­альной жидкости отсутствует вяз­кость, следовательно, нет трения между слоями движущейся жид­кости. Поэтому в сечении 1—1 струйки идеальной жидкости все скорости одинаковы и эпюра ско­ростей на рис. 3.2, а имеет прямоугольную форму.

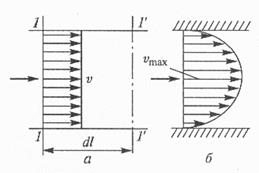Через время dt сечение 1—1, площадь которого обозначим S, займет новое положение 1’-1’, смещенное относительно началь­ного положения на расстояние dl. При этом новое сечение 1’—1’ (как и начальное 1—1) будет

Рис 3.2 Эпюры распределения скоростей плоскостью, так как при

идеальной (а) и реальной (б) жидкостей равных скоростях все частицы

жидкости продвинутся на равное расстояние dl. Тогда за время dt через сечение 1—1 переместится объем жидкости W= dlS, а объемный расход составит

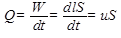
Таким образом, при течении идеальной жидкости существует удобная зависимость, связывающая основные кинематические и геометрические параметры струйки (или потока): объемный расход Q, скорость жидкости v и площадь сечения S.

При течении потока реальной жидкости между ее слоями возникает трение. Крайние слои жидкости из-за трения о стенку имеют практически нулевую скорость (рис. 3.2, б). По мере удаления от стенки каждый последующий слой приобретает более высокую скорость, и максимальная скорость в сечении v_max отмечается в середине потока. Следовательно, происходит перераспределение скоростей по сечению площадью S, что затрудняет определение математической взаимозависимости между основными геометри­ческими и кинематическими параметрами потока реальной жид­кости.

Для устранения отмеченного затруднения введем понятие сред­ней скорости в сечении v_cp, под которой будем понимать скорость, удовлетворяющую следующему равенству:

Q=uсрS. (3.2)

Тогда v_cp – это условная скорость, существующая в каком- то промежуточном слое потока реальной жидкости. Обычно она меньше максимальной скорости v_max и лежит пределах 0,5v_max ≤ v_cp < v_max. Таким образом, зависимость (3.2) связывает основные геометрические и кинематические параметры потока реальной вязкой жидкости.

При расчете гидравлических систем широко используется уравне­ние, которое можно получить из равенства расходов в двух сечения одного потока. На рис. 3.3 приведен и поток жидкости. Очевидно, что (исходы в сечениях 1— 1 и 2— 2 это- I с I потока жидкости одинаковы, т. е. Q₁, = Q₂. Тогда с учетом (3.2) получим зависимость

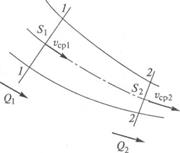
Рис. 3.3 Схема потока жидкости

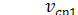S_l =u_ср2S₂, (3.3)

связывающую основные геометрические и кинематические пара­метры потока в этих сечениях.

Уравнение (3.3) получило название уравнения неразрывности, или уравнения расхода. Оно позволяет определить среднюю скорость в любом сечении потока жидкости (например, v_cp1), если известны хотя бы одна из средних скоростей этого потока (например, u_ср2) и его геометрические размеры. Уравнение (3.3) является законом сохранения вещества для потока (или струйки) жидкости, записанное при условии постоянства плотности жидкости в пределах рассматриваемого потока.

И заключение следует отметить, что при расчетах машиностро­ительных гидросистем в большинстве случаев индекс «ср» и тер­мин «средняя» опускают, а говорят о скорости в сечении потока. При этом под скоростью понимают ее среднюю величину.

Поиск по сайту: