Работа расширения или сжатия газа

Одним из основных термодинамических процессов, совершающихся в большинстве тепловых машин, является процесс расширения газа с совершением работы. Легко определить работу, совершаемую при изобарном расширении газа.

Если при изобарном расширении газа от объема V ₁ до объема V ₂ происходит перемещение поршня в цилиндре на расстояние l (рис. 7.3), то работа A', совершенная газом, равна

, (7.27)

где p — давление газа, — изменение его объема.

3

Рис 7.3 Рис 7.4

Как видно из рисунка 7.4, при изображении изобарного процесса расширения газа в координатных осях p, V площадь фигуры, ограниченной графиком процесса, координатами V ₁ и V ₂, осью абсцисс, пропорциональна работе газа A'.

Работа при произвольном процессе расширения газа. Произвольный процесс расширения газа от объема V ₁ до объема V ₂ можно представить как совокупность чередующихся изобарных и изохорных процессов.

При изохорных процессах работа равна нулю, так как поршень в цилиндре не перемещается. Работа при изобарных процессах пропорциональна площади фигуры на диаграмме p, V под соответствующим участком изобары (рис. 7.5).

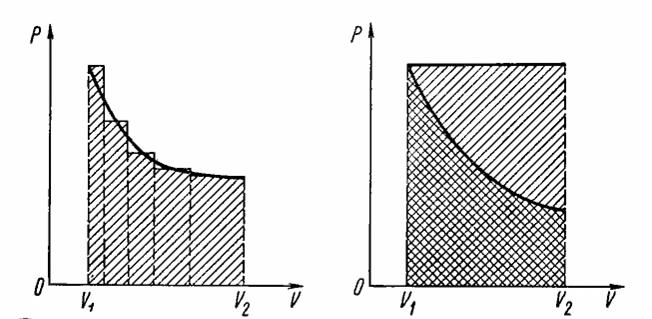
Рис. 7.5 Рис. 7.6

Следовательно, работа при произвольном процессе расширения газа прямо пропорциональна площади фигуры под соответствующим участком графика процесса на диаграмме p, V.

Работа при изотермическом расширении газа. Сравнивая площади фигур под участками изотермы и изобары (рис. 7.6), можно сделать вывод, что расширение газа от объема V ₁ до объема V ₂ при одинаковом начальном значении давления газа сопровождается в случае изобарного расширения совершением большей работы.

Работа при сжатии газа. При расширении газа направление вектора силы давления газа совпадает с направлением вектора перемещения, поэтому работа A', совершенная газом, положительна (A' > 0), а работа А внешних сил отрицательна: A = - A' < 0.

При сжатии газа направление вектора внешней силы совпадает с направлением перемещения, поэтому работа А внешних сил положительна (A > 0), а работа A', совершенная газом, отрицательна (A' < 0).

Адиабатный процесс. Кроме изобарного, изохорного и изотермического процессов, в термодинамике часто рассматриваются адиабатные процессы.

Адиабатным процессом называется процесс, происходящий в термодинамической системе при отсутствии теплообмена с окружающими телами, т. е. при условии Q = 0.

Отсутствие теплообмена с окружающей средой может быть обеспечено хорошей теплоизоляцией газа. Быстрые процессы расширения или сжатия газа могут быть близкими к адиабатному и при отсутствии теплоизоляции, если время, за которое происходит изменение объема газа, значительно меньше времени, необходимого для установления теплового равновесия газа с окружающими телами.

Примерами адиабатных процессов могут служить процессы сжатия воздуха в цилиндре воздушного огнива, в цилиндре двигателя внутреннего сгорания. В соответствии с первым законом термодинамики, при адиабатном сжатии изменение внутренней энергии газа равно работе внешних сил А:

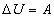(7.28)

Так как работа внешних сил при сжатии положительна, внутренняя энергия газа при адиабатном сжатии увеличивается, его температура повышается.

При адиабатном расширении газ совершает работу A' за счет уменьшения своей внутренней энергии:

, (7.29)

поэтому температура газа при адиабатном расширении понижается. Это можно обнаружить в следующем опыте. Если в бутылку, содержащую насыщенный водяной пар, накачивать с помощью насоса воздух, то пробка вылетает (рис. 7.7).

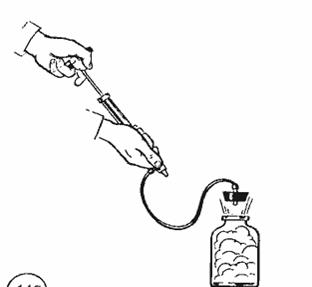
Рис. 7.7

Работа A' по выталкиванию пробки совершается воздухом за счет уменьшения его внутренней энергии, так как расширение воздуха происходит за очень короткое время и теплообмен с окружающей средой не успевает произойти. Образование капель тумана доказывает, что при адиабатном расширении воздуха его температура понизилась и опустилась ниже точки росы.

График адиабатного процесса. Поскольку при адиабатном сжатии температура газа повышается, то давление газа с уменьшением объема растет быстрее, чем при изотермическом процессе. Понижение температуры газа при адиабатном расширении приводит к тому, что давление газа убывает быстрее, чем при изотермическом расширении.

График адиабатного процесса в координатных осях p, V представлен на рисунке 1.8. На том же рисунке для сравнения приведен график изотермического процесса.

Рис. 7.8

Вну́тренняя эне́ргия тела (обозначается как E или U) — полная энергия этого тела за вычетом кинетической энергии тела как целого и потенциальной энергии тела во внешнем поле сил. Следовательно, внутренняя энергия складывается из кинетической энергии хаотического движения молекул, потенциальной энергии взаимодействия между ними и внутримолекулярной энергии.

Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход.

Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:

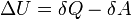
где

— подведённая к телу теплота, измеренная в джоулях

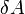— работа, совершаемая телом против внешних сил, измеренная в джоулях

Эта формула является математическим выражением первого начала термодинамики

Для квазистатических процессов выполняется следующее соотношение:

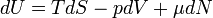
где

— температура, измеренная в кельвинах

— энтропия, измеренная в джоулях/кельвин

— давление, измеренное в паскалях

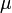— химический потенциал

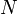— количество частиц в системе

Идеальные газы

Согласно закону Джоуля, выведенному эмпирически, внутренняя энергия идеального газа не зависит от давления или объёма. Исходя из этого факта, можно получить выражение для изменения внутренней энергии идеального газа. По определению молярной теплоёмкости при постоянном объёме, . Так как внутренняя энергия идеального газа является функцией только от температуры, то

. (7.30)

Эта же формула верна и для вычисления изменения внутренней энергии любого тела, но только в процессах при постоянном объёме (изохорных процессах); в общем случае C_V (T, V) является функцией и температуры, и объёма.

Если пренебречь изменением молярной теплоёмкости при изменении температуры, получим:

Δ U = ν C_V Δ T, (7.31)

где ν — количеств о вещества, Δ T — изменение температуры.

Термодинамические процессы: изохорный, изобарный, изотермический, адиабатный, политропный

Изохорный процесс (v=const)

Такой процесс может совершаться рабочим телом, находящимся в цилиндре при неподвижном поршне, если к рабочему телу подводится теплота от источника теплоты (см. рис.7.9) или отводится теплота от рабочего тела к холодильнику. При изохорном процессе выполняется условие dv=0 или v=const. Уравнение изохорного процесса получим из уравнения состояния идеального газа при v=const. В pv -координатах график процесса представляет собой прямую линию, параллельную оси p. Изохорный процесс может протекать с повышением давления (процесс 1-2) и с понижением (процесс 1-2’).

Запишем для точек 1 и 2 уравнения состояния: p₁·v=R·T₁; p₂·v=R·T₂. Следовательно, для изохорного процесса

Приращение внутренней энергии газа

Работа газа:

так как dv=0.

Энтальпия газа i_v=u+p·v, а di_v=du+d(p·v)=du+p·dv+v·dp=du+v·dp. Поэтому

Энтропия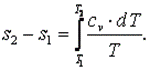

То есть

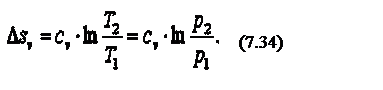
Изобарный процесс (p=const)

В p-v координатах график процесса представляет собой прямую линию параллельную оси v (рис. 7.10). Изобарный процесс может протекать с увеличением объёма (процесс 1-2) и с уменьшением (процесс 1-2’). Запишем для точек 1 и 2 уравнения состояния: p·v₁=R·T₁; p·v₂=R·T₂.

Следовательно, для изобарного процесса

Приращение внутренней энергии газа 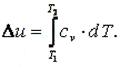Работа газа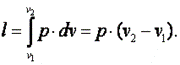

Так как p·v₂=R·T₂, а p·v₁=R·T₁, то l=R·(T₂-T₁). Следовательно, газовая постоянная имеет определённый физический смысл: это работа 1 кг газа в изобарном процессе при изменении температуры на один градус. Следует, что в изобарном процессе q=c_p·(T₂-T₁). В соответствии с первым законом термодинамики для изобарного процесса можно записать dq=du+p·dv= du+d(p·v)=di. Поэтому в изобарном процессе di=q=c_p·(T₂-T₁). Из соотношений, характеризующих изобарный процесс, вытекает известное уравнение Майера. Так как dq=c_p·dT=c_v·dT+dl=c_v·dT+R·dT, то R=c_p-c_v.

Можно показать, что в изобарном процессе энтропия газа

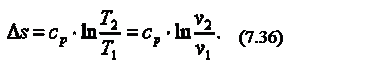
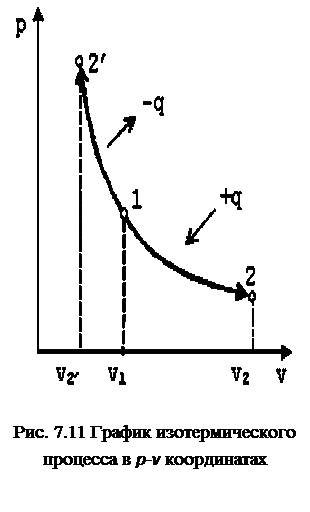
Изотермический процесс (T=const)

В p-v координатах график процесса изображается равнобокой гиперболой (рис. 7.11). Изотермический процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).

Запишем для точек 1 и 2 уравнения состояния p₁·v₁=R·T; p₂·v₂=R·T. Следовательно, для изотермического процесса p₁·v₁=p₂·v₂=const.

Приращение внутренней энергии газа:

Работа газа

Теплота, подводимая в процессе

Изменение энтальпии газа Δi=Δu+Δ(p&middotv)=0.

Изменение энтропии газа

Адиабатный процесс

Адиабатный процесс – это процесс, при котором рабочее тело не обменивается теплотой с окружающей средой (dq=0). Для получения графика процесса в p-v координатах выполним некоторые преобразования.

В соответствии с первым законом термодинамики, где с – теплоёмкость термодинамического процесса. Тогда можно записать, что

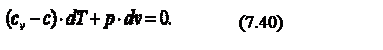
Продифференцируем уравнение состояния идеального газа и запишем

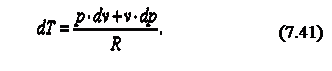
Так как R=c_p-c_v, то выражение (7.41) можно переписать с учётом (7.42) следующим образом:

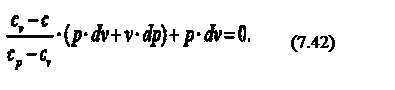
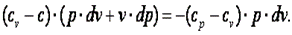Выполним преобразования выражения

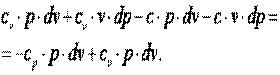
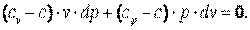
(7.44)

(7.45)

Разделим выражение (7.44) и получим:

Обозначим 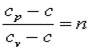, тогда

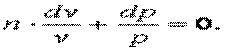
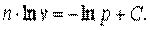
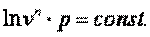
Следовательно

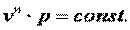
(7.46)

В адиабатном процессе dq=0, то есть c&middotdT=0. Поэтому c=0. Значит в адиабатном процессе . Эту величину принято обозначать буквой 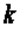и называть показателем адиабаты.

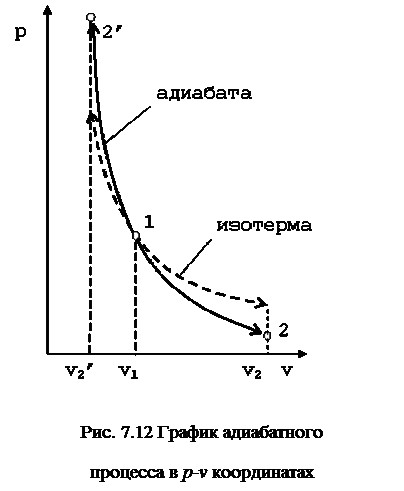Поэтому в p-v координатах адиабатный процесс изображается неравнобокой гиперболой v^k&middotp=const (рис. 7.12). Так как k>1, то адиабата проходит круче гиперболы. Адиабатный процесс может протекать как с увеличением объёма (процесс 1-2), так и с уменьшением объёма (процесс 1-2’).

Запишем для точек 1 и 2 уравнения состояния Так как в адиабатном процессе p₁&middotv₁^k=p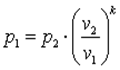₂&middotv₂^k, то , , .

Приращение внутренней энергии газа.

Так как 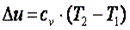, а , то , а .

Поэтому

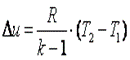
(7.47)

Работа газа в адиабатном процессе выполняется за счёт его внутренней энергии. Так как в адиабатном процессе отсутствует обмен теплотой с окружающей средой, то в соответствии с первым законом термодинамики имеем l+Δu=0 или l=-Δu. Поэтому

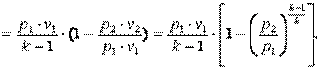
(7.48)

Изменение энтальпии газа в адиабатном процессе может быть определено исходя из следующих соображений:

Так как, то в итоге получим

Энтропия газа в адиабатном процессе не изменяется, так как dq=0. Поэтому в T-s координатах адиабатный процесс изображается прямой линией, параллельной оси температур.

Политропный процесс

Политропным процессом называется любой произвольный процесс изменения состояния рабочего тела, происходящий при постоянной теплоёмкости с_п.

Для получения графика политропного процесса в p-v координатах будем придерживаться тех же рассуждений, что и при получении графика адиабатного процесса. Заменим в соотношениях, полученных при изучении адиабатного процесса, обозначение теплоёмкости с на с_п и обнаружим, а . В дальнейшем всё, что написано об адиабатном процессе, можно распространить на описание политропного процесса, заменяя в выражениях k на n.

Покажем, что адиабатный процесс делит все процессы на две группы: на процессы, в которых теплоёмкость больше нуля, и на процессы, в которых теплоёмкость меньше нуля.

Так как 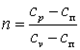, то можно записать

;

;

;

.

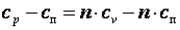Из последнего выражения видно, что при n>k c_п>0, а при k>n>1 c_п<0.

В заключение отметим, что все рассмотренные ранее процессы – это частные случаи политропного процесса.

При n=k имеем адиабатный процесс.

При n=0 имеем р₁·v₁⁰=р₂·v₂⁰, то есть изобарный процесс (p₁=p₂).

При n=1 имеем р₁·v₁= р₂·v₂, то есть изотермический процесс.

При n=∞ имеем

или 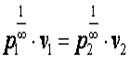, что равносильно

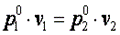
или 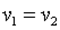, то есть изохорный процесс.

Поиск по сайту: