 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение Бернулли для потока реальной жидкости
Пусть поток реальной жидкости, обладающей вязкостью, движется в русле, ограниченном неподвижными стенками. При этом возникает трение, что приводит к существенной неравномерности распределения скоростей по сечению потока (рис. 3.5), а также к потерям энергии при перемещении жидкости от одного сечения к другому.
Получим уравнение Бернулли для потока реальной жидкости, основываясь на том, что оно является законом сохранения энергии для движущейся жидкости. Вывод этого уравнения проведем в два этапа. На первом этапе учтем неравномерность распределения скоростей по сечению потока, а на втором учтем и потери энергии.
При выводе будем считать, что в пределах выбранных сечений
гидростатический напор остается постоянным:
Z +  = const. (3.7)
= const. (3.7)

Рис. 3.5. Схема потока реальной жидкости
Это справедливо для сечений с параллельно струйным течением жидкости, т.е. когда эти сечения являются плоскими. Поэтому уравнение которое будет получено ниже, может использоваться для плоских или близких к ним сечений.
На первом этапе определим формулу для вычисления мощности N потока реальной жидкости в его сечении. Вычисление этого параметра затруднено тем, что из-за перераспределения скоростей (см. рис. 3.5) разные слои жидкости несут различное количество энергии. Для определения мощности N в сечении (например, в сечении 1— 1 на рис. 3.5) выберем струйку жидкости бесконечно милой поперечной площади dS, в пределах которой скорость жидкости будем считать постоянной, равной v. Тогда полный напор (или полная удельная энергия) в сечении струйки
H=Z+ 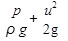 (3.8)
(3.8)
Мощность струйки dN в сечении площадью dS равна произведению удельной энергии Н и веса жидкости, которую проносит поток через это сечение в единицу времени, т.е. элементарного носового расхода dQG. Тогда с учетом (3.6) и (3.1) получим математическую зависимость для мощности струйки
dN=GdQg=(Z+ 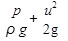 )pgdQ (3.9)
)pgdQ (3.9)
Мощность всего потока в сечении найдем, просуммировав мощности всех элементарных струек, т.е. вычислив интеграл по площади S от выражения (3.9):

После математических преобразований зависимость для мощности потока реальной жидкости принимает следующий вид:
N=pg(z+  )Q (3.10)
)Q (3.10)
где α — безразмерный коэффициент, определяемый по формуле
 (3.11)
(3.11)
Этот коэффициент, называемый коэффициентом Кориолиса, учитывает неравномерность распределения скорости жидкости сечении реального потока. Если числитель и знаменатель в формуле (3.11) умножить на р/2, то станет очевидно, что коэффициент а есть отношение действительной кинетической энергии реального потока в данном сечении к кинетической энергии того же потока в том же сечении, но посчитанной по средней скорости жидкости в данном сечении. В этом заключается физический смысл коэффициента Кориолиса.
Алгебраическое выражение, ограниченное скобками в (3.10), принято называть средним значением полного напора в сечении реального потока, т.е.
Hср=z+  (3.12)
(3.12)
Средний напор Hср широко используется в практических расчетах, так как является важнейшим параметром, характеризующим механическую энергию (или мощность) потока реальной жидкости. Для подтверждения этого решим уравнение (3.10) относительно Hср с учетом (3.12). Тогда получим
Hср=  . (3.13)
. (3.13)
Из анализа зависимости (3.13) следует, что при постоянном расходе Q средний напор Hср пропорционален мощности N ив пределах данного потока однозначно определяет эту мощность. Поэтому средний напор Hср, вычисляемый с учетом неравномерности распределения скоростей в сечении по формуле (3.12), в дальнейшем будем использовать в качестве основного параметра, характеризующего механическую энергию потока реальной жидкости.
Учтем теперь потери энергии, возникающие при движении жидкости. В реальных потоках из-за этих потерь среднее значение полного напора в в конечном сечении всегда меньше, чем в начальном сечении, т.е. Hср1 > Нср2. Поэтому при записи уравнения баланса (средних напоров) в его правую часть добавляют слагаете ∑hпот учитывающее потери удельной энергии. Тогда уравнение баланса принимает вид
Hср1 = Нср1 + ∑hпот,
или с учетом (3.12)
z1+  +α1
+α1  =z2+
=z2+ 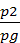 +α1
+α1  +∑hпот (3.14)
+∑hпот (3.14)
Уравнение (3.14) носит название уравнения Бернулли для потока реальной жидкости.
При использовании этого уравнения в дальнейшем индексы «ср» будем опускать. Сравним уравнение Бернулли для струйки идеальной жидкости (3.6) и уравнение для потока реальной жидкости (3.14). Из этого сравнения следует, что в последнем уравнении дополнительно присутсвуют α и ∑hпот.
При равномерном распределении скоростей по сечению потока α=1 (поток идеальной жидкости). В потоках реальной жидкости коэффициент Кориолиса в большинстве случаев лежит в пределах 1<α≤2.
Суммарная потеря полного напора ∑hпот на участке между начальным и конечным сечениями складывается из суммы потерь удельной энергии во всех гидравлических сопротивлениях, расположенных на рассматриваемом участке потока. В гидравлике эти потери энергии принято делить на две группы: местные потери и потери на трение по длине. Местные потери hM — это потери в местных (локальных) гидравлических сопротивлениях, к которым относятся поворот, сужение или расширение потока, а также различные гидравлические устройства (вентили, жиклеры и т.д.). Потери в большинстве этих сопротивлений вызваны вихреобразованием. Как показывает практика, они пропорциональны квадрату скорости жидкости, а для оценки их величины используется формула Вейсбаха
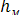 = ζ
= ζ 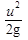 (3.15)
(3.15)
где С, — безразмерный коэффициент, определяющий потери в данном местном сопротивлении; v — средняя скорость в трубопроводе, в котором установлено местное сопротивление.
Второй вид гидравлических потерь — потери на трение по длине  — это потери, которые имеют место в длинных прямых трубах постоянного сечения. Потери на трение по длине вызваны как внутренним трением в жидкости, так и трением о стенки трубы, Эти потери пропорциональны длине трубы l и обратно пропорциональны ее диаметру d. Они имеют достаточно сложную зависимость от средней скорости жидкости v (это будет рассмотрено позднее), но во всех случаях для их оценки может быть использована универсальная для гидравлики формула Дарси
— это потери, которые имеют место в длинных прямых трубах постоянного сечения. Потери на трение по длине вызваны как внутренним трением в жидкости, так и трением о стенки трубы, Эти потери пропорциональны длине трубы l и обратно пропорциональны ее диаметру d. Они имеют достаточно сложную зависимость от средней скорости жидкости v (это будет рассмотрено позднее), но во всех случаях для их оценки может быть использована универсальная для гидравлики формула Дарси
Hтр=λ  (3.16)
(3.16)
где λ — безразмерный коэффициент потерь на трение по длине, который принято называть коэффициентом Дарси.
Следует отметить, что определение потерь энергии при расчете!! гидравлических систем является одной из наиболее важных проблем гидравлики.
Поиск по сайту: