 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Уравнение Бернулли для струйки идеальной жидкости
Рассмотрим установившееся течение элементарной струйки идеальной жидкости, находящейся под действием лишь одной массовой силы — силы тяжести (рис. 3.4). В рассматриваемом случае в жидкости могут действовать нормальные напряжения сжатия (давление), но не могут действовать касательные напряжения (трение), так как у жидкости отсутствует вязкость.
Для вывода уравнения Бернулли выберем два сечения 1—1 и 2 -2, а также произвольную горизонтальную поверхность 0—0. Будем считать, что в сечении 1—1 площадью S1 существует
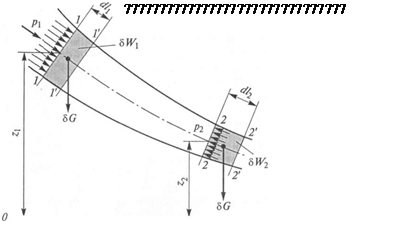 |  | ||
скорость жидкости v1 и действует давление p1 а его центр тяжести располагается на высоте Z1 относительно выбранной поверхности
0-0. Сечение 2—2 характеризуется аналогичными параметрами, но с индексом «2» (S2,u2,P2 и z2).
Пусть за время dt участок струйки, ограниченный сечениями 1-1 и 2-2 сдвинулся и занял новое положение, ограниченное сечениями 1’—1’ и 2'—2'. Тогда первое сечение переместилось на расстояние dl2 а второе сечение — на расстояние dl2. При этом можно условно считать, что часть ограниченного объема жидкости осталась на месте (объем между сечениями Г—1' и 2—2),; другая часть между сечениями 1—1 и Г—Г (на рис. 2.4 затемнена переместилась на место между сечениями 2—2 и 2'—2' (на рис. 2.4 также затемнена), т.е. объемы затемненных участков равны:
δW1=S1dl1= δW2=S2dl2= δW.
Следовательно, равны и массы этих объемов (δm), а также одинаковы их веса (δG).
Для вывода уравнения Бернулли применим к жидкому телу между сечениями 1—1 и 2— 2 теорему механики об изменении кинетической энергии, согласно которой изменение кинетической энергии тела равно работе сил, приложенных к телу.
Как следует из сказанного ранее, кинетическая энергия участка жидкости между сечениями 1—1' и 2—2 за время dt не изменилась, так как этот участок условно можно считать неподвижным. Тогда изменение кинетической энергии всего жидкого тела будет определяться разностью кинетических энергий выделенных объемов (участков, затемненных на рис. 3.4), а точнее, изменением и: скоростей, так как их массы одинаковы, т.е.
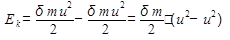
Работу за отмеченный промежуток времени совершают силы тяжести и силы давления. При оценке работы сил тяжести также Пудем учитывать условную неподвижность участка жидкости между сечениями 1’—1’ и 2—2. Тогда работа сил тяжести LG определится перемещением веса δG на расстояние (z, - z2):

Работа сил давления Lp будет складываться из двух величин: работы положительной силы и работы отрицательной силы. Первая, равная произведению давления p1 на площадь Su способствует сдвигу сечения 1—1 на расстояние dlu а вторая, равная произведению давления р2 на площадь S2, препятствует перемещению сечения 2—2 на расстояние dl2, т.е.
Lp = pxS\dlx - p2S2dl2 = - p2bW2 = bW{pi - p2).
Приравняв сумму работ сил тяжести Lc и давления Lp к измерению кинетической энергии тела Ек, получим
 G(z1-z2)+
G(z1-z2)+  W(p1-p2)=
W(p1-p2)= 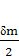 (
(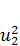 -
- 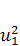 ) (3.4)
) (3.4)
Разделим каждый член уравнения (3.4) на вес  G. Тогда получим
G. Тогда получим
(z1-z2)+ 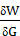 (p1-p2)=
(p1-p2)= 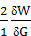 (
(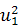 -
- 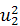 ) (3.5)
) (3.5)
В последнее математическое выражение входят объем 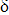 W, масса δт и вес δG одного и того же количества жидкости, которые связаны между собой (5G = SWpg = 8mg). После математических преобразований окончательно получим уравнение Бернулли для струйки идеальной жидкости:
W, масса δт и вес δG одного и того же количества жидкости, которые связаны между собой (5G = SWpg = 8mg). После математических преобразований окончательно получим уравнение Бернулли для струйки идеальной жидкости:
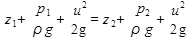 (3.6)
(3.6)
Каждый член уравнения (3.6) представляет собой определенный вид удельной энергии (энергии, отнесенной к единице веса жидкости и измеряется в линейных единицах (в СИ это метры).
Величины Z1 и z.2 являются удельными энергиями положения жидкости в сечениях. Их еще называют нивелирными высотами.
Отношения 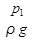 и
и 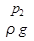 представляют собой удельные энергии
представляют собой удельные энергии
давления (сжатия) жидкости в сечениях и называются еще пьезометрическими высотами.
Суммы величин Z1+ 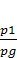 и
и 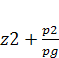 являются удельными потенциальными энергиями жидкости в сечениях и называются также и гидравлике гидростатическими напорами.
являются удельными потенциальными энергиями жидкости в сечениях и называются также и гидравлике гидростатическими напорами.
Последние слагаемые в обеих частях уравнения Бернулли (3.6)
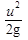 и
и 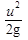 представляют собой удельные кинетические энергии
представляют собой удельные кинетические энергии
жидкости в сечениях и называются еще скоростными напорами.
Наконец, суммы 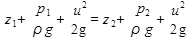 являются полными удельными энергиями в каждом сечении струйки жидкости. В гидравлике их принято называть полными напорами и обозначать символом
являются полными удельными энергиями в каждом сечении струйки жидкости. В гидравлике их принято называть полными напорами и обозначать символом
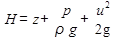
После рассмотрения энергетического смысла каждого слагаемого зависимости (3.6) можно сформулировать энергетический смысл всего уравнения Бернулли так: в потоке идеальной жидкости ее полная удельная энергия в сечении есть величина постоянная.
Таким образом, полученное уравнение Бернулли является законом сохранения энергии для струйки идеальной жидкости.
Поиск по сайту: