Определение деформаций на примере операций осадки и выдавливания

Деформированное состояние в точке описывается тензором деформации:

. (2.1)

Компоненты ε_X, ε_Y, ε_Z характеризуют линейные деформации волокон, расположенных по осям x, y, z (т.е. относительные удлинения или относительные укорочения), а компоненты ε_XY, ε_YZ, ε_YZ - углы поворота двух взаимно перпендикулярных до деформации волокон (или деформации сдвига).

Для компонента деформаций сдвига справедливы равенства:

(2.2)

При повороте системы координат все компоненты тензора деформации преобразуются по определенным линейным относительно направляющих косинусов соотношениям. В теории деформации и линейных преобразований доказывается, что из всех возможных направлений осей координат существует тройка взаимно перпендикулярных направлений (главных направлений), относительно которых все сдвиговые компоненты деформации равны нулю. Главные направления деформаций определяются тремя величинами, независящими от положения системы координат и называемыми инвариантами.

Первый инвариант используется для записи условия постоянства объема деформируемого металла:

Второй инвариант тензора деформации, учитывает линейные и сдвиговые имеет вид:

.

Величина, пропорциональная корню квадратному из второго инварианта, называется интенсивностью деформаций и используется для характеристики деформаций в общем случае деформированного состояния:

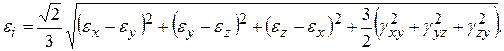(2.3)

В случае, когда компоненты деформаций малы по сравнению с единицей, а углы поворота малы настолько, что квадратами и произведениями их по сравнению с компонентами деформации можно пренебречь, компоненты деформации связаны с компонентами перемещений линейными зависимостями (формулами Коши).

В индексных обозначениях формулы Коши могут быть записаны в виде:

(2.4)

где i, j = 1, 2, 3, x₁ = x, x₂ = y, x₃ = z или в обычных обозначениях:

(2.5)

В частности при осадке при малых деформациях и отсутствии трения на торцах образца линейная деформация (укорочение волокна) по оси z рассчитывается по формуле:

(2.6)

С учетом условия (2.3) сохранения объема при пластической деформации и в силу симметрии:

следовательно:

(2.7)

Истинные (конечные) ε_Zи деформации определяются интегрированием:

. (2.8)

Работа деформации при осадке:

(2.9)

где P – усилие деформирования, F – площадь поперечного сечения образца, p – удельное давление, p_ср – среднее удельное давление.

Пренебрегая упрочнением (что для свинцового образца при комнатной температуре вполне приемлемо), будем считать среднее удельное давление равным пределу текучести:

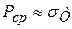. (2.11)

Таким образом, предел текучести σ_T можно определить по измеренной в опыте на сжатие (то есть при осадке образца) работе деформации:

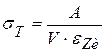. (2.12)

При выдавливании материал получает значительную и неоднородную деформацию. Величина и вид деформации зависят от соотношения площадей поперечного сечения заготовки до деформации и после истечения через матрицу, а также от сил трения заготовки о поверхности матрицы и контейнера. Деформации оказывают большое влияние на работу деформации и деформирующее усилие. В связи с этим анализ деформированного состояния выдавленной заготовки представляет важную проблему.

Для экспериментального изучения деформаций при выдавливании может быть использован метод накатных сеток. Согласно этому методу цилиндрический свинцовый образец разрезается вдоль по диаметральной плоскости и на плоскости полуцилиндров наносится квадратная делительная сетка (рис. 2.6)

Рис. 2.6. Цилиндрический образец, разрезанный по диаметральной плоскости, после нанесения на эту плоскость квадратной делительной сетки

После деформации (выдавливания) координатная делительная сетка и контуры самого образца изменяются (рис. 2.7).

Рис. 2.7. Схема изменения делительной сетки образца после выдавливания

Представим сложное деформированное состояние в виде суммы двух более простых: растяжения (рис. 2.8) и неоднородного осесимметричного сдвига (рис. 2.9):

(2.12)

Рис. 2.8. Схема деформации растяжения цилиндрического образца
(в диаметральной плоскости)

Рис. 2.9. Схема неоднородного осесимметричного сдвига прямоугольного элемента

делительной сетки в диаметральной плоскости. А и В – значения координаты Z измеряемой

линии без учета сдвига и с учетом сдвига

Поскольку при пластической деформации металлов объем деформируемого металла остается практически неизменным, справедливо соотношение:

, (2.13)

откуда , (2.14)

где λ – вытяжка металла.

Определим относительное удлинение ε_z по оси z:

. (2.15)

Однако эта характеристика деформации используется только для малых деформаций или приращений деформаций. Для конечных деформаций необходимо применять истинные, то есть интегральные характеристики деформации:

. (2.16)

Остальные линейные компоненты тензора деформации определяются из условий неизменности объема деформации и условия симметрии (осесимметричности) деформации:

(2.17)

Таким образом, тензор деформации растяжения в приложении к рассматриваемому примеру выдавливания имеет вид:

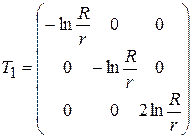. (2.18)

Деформации неоднородного осесимметричного сдвига определяются путем дифференцирования перемещений U_z(ρ):

, (2.19)

где ρ – переменная в полярных координатах (φ, ρ, z).

Тензор деформации неоднородного осесимметричного сдвига имеет вид:

, (2.20)

где . (2.21)

Тензор суммарной деформации определим суммированием:

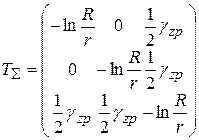. (2.22)

Таким образом, интенсивность деформаций при выдавливании рассчитывается как:

, (2.23)

Поиск по сайту: