НАДЕЖНОСТИ

Показатели надежности прибора можно рассчитать, если известен закон распределения и его основные параметры. В табл. 1 приведены основные показатели надежности для произвольного закона распределения случайных величин. На практике при анализе надежности широкое распространение нашел случай, когда интенсивность отказов полагается постоянной во времени. Этот случай характерен для изделий со случайными, не связанными между собой отказами, когда отказы не обусловлены деградацией прибора со временем. В этом случае λ(t) = λ, где λ, - некоторая постоянная величина.

Распределение вероятности отказов, соответствующее такой λ-характеристике, называется экспоненциальным.

В табл. 2 приведены основные показатели надежности элемента для экспоненциального распределения вероятности отказа.

Как видно из приведенных формул, показатели надежности для экспоненциального распределения очень легко рассчитываются. Это - одна из.причин, определивших его популярность.

Определим гамма-процентную наработку до отказа при

экспоненциальном распределении:

Положим γ = 90 %. Это означает, что не менее 90 % приборов из рассматриваемой нами совокупности должны безотказно работать в течение времени t_γ (или вероятность безотказной работы совокупности приборов в течение времени t_γдолжна быть не ниже 0,9). С учетом этого получим

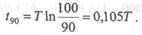
Полученный результат показывает, что гамма-процентная наработка при γ = 90 % составит всего примерно 0,1 от средней наработки до отказа.

Рассмотрим еще один пример.

Допустим, что мы имеем дело с аппаратурой, построенной на идентичных приборах, имеющих экспоненциальное распределение с интенсивностью отказов 10^-7 ч^-1. Определить время безотказной работы элемента с вероятностью γ = 99,9 %.

Средняя наработка до отказа из расчета на один прибор составит:

Тогда время безотказной работы составит t_γ = 10 005 ч, или почти один год и два месяца.

Экспоненциальное распределение уникально в том смысле, что ожидаемый характер отказов никак не меняется на протяжении всего срока службы изделия. Предшествующее использование прибора никак не влияет на его работоспособность в последующие моменты времени, а определяется длиной интервала ∆t Это означает, что в каком бы месте числовой оси мы не выбрали временной интервал ∆t, если к его началу отказов приборов не наблюдалось, то показатели надежности останутся такими же, какими были на начальный момент времени t = 0. Это свойство изделия однозначно определяет условия применимости экспоненциального распределения.

Рассмотрим пример.

Пример: Пусть элемент имеет экспоненциальное распределение времени работы до отказа с параметром распределения λ = 2,5-1 0^-3 1/ч. Вычислить основные показатели надежности.

Решение:

1. Вероятность безотказной работы за время t = 2000 ч

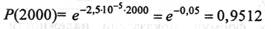
2. Вероятность отказа за время t₀ = 2000 ч: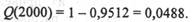

3. Вероятность безотказной работы в интервале времени от t = 500 ч до t + to = 2500 ч при условии, что элемент проработал безотказно 500 ч.

4. Вероятность отказа в интервале времени от t = 500 ч до t + t₀ = 2500 ч при условии, что элемент проработал безотказно 500 ч.

5. Среднее время работы до отказа

6.Время безотказной работы, с вероятностью γ = 90%

7. Плотность вероятности отказов

Для описания показателей надежности полупроводниковых приборов и микросхем на начальном этапе эксплуатации часто используется распределение Вейбулла - Гнеденко, характеризуемое двумя параметрами: параметром масштаба а и параметром формы b. Показатели надежности определяются с использованием следующих выражений:

Экспоненциальное распределение является частным случаем распределения Вейбулла - Гнеденко и реализуется при b = 1.

Особенностью этого распределения является то, что с изменением параметра формы b изменяется и характер зависимости показателей надежности от времени. Так, например, при b < 1 интенсивность отказов λ(t) будет монотонно убывающей функцией, при b > 1 монотонно возрастающей. Данное свойство распределения позволяет соответствующим подбором параметров а и b обеспечить хорошее совпадение результатов опытных данных с аналитическими выражениями показателей распределения.

Графическое изображение зависимости показателей надежности от времени для рассмотренных распределений приведено в табл. 3.

Определенный интерес представляет сравнение показателей надежности для нормального и экспоненциального распределений при одном и том же значении средней наработки до отказа. Графическая зависимость вероятности безотказной работы от времени для этих двух распределений представлена на рис. 5.

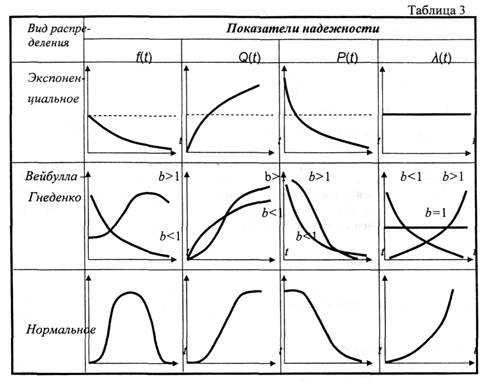
Из рассмотрения данных зависимостей следует, что вероятность безотказной работы при экспоненциальном распределении с течением времени (при малых значениях t) уменьшается быстрее, чем при нормальном. По достижении момента времени, равного средней наработке до отказа, при экспоненциальном распределении вероятность безотказной работы P(t) будет равна 0,37, а при нормальном распределении - 0,5. Это наглядно показывает, что более высокие показатели надежности в интервале времени (0; Т) имеют приборы, случайное время безотказной работы которых подчиняется нормальному распределению, чем приборы с экспоненциальным распределением.

Заштрихованный участок рисунка протяженностью 0,1 T представляет собой промежуток времени, в пределах которого обеспечивается максимальный уровень вероятности безотказной работы. При вероятности безотказной работы 0,95 и выше различия между законами распределения становятся несущественными, поэтому применяется наиболее простое для описания показателей надежности приборов экспоненциальное распределение.

Поиск по сайту: