Статика. для студентов очной и заочной форм обучения специальностей:

ТЕХНОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ

Д.А. СКОТНИКОВ, А.В. АНИСИМОВ А.А. МАРЬИНА

Прикладная механика

Учебное пособие

для студентов очной и заочной форм обучения специальностей:

260301 – «Технология мяса и мясных продуктов»

260303 – «Технология молока и молочных продуктов»

260501 – «Технология продуктов общественного питания»

240901 – «Биотехнология»

Саратов

ООО Издательский Центр «Наука»

УДК 539.3/.6(075,8)

ББК 30.121.73

С 64

Скотников Д.А., Анисимов А.В., Марьина А.А.

С 64 Детали машин: Учеб. пособие. – Саратов: ООО Издательский Центр

«Наука», 2010. - 308 с.

ISBN

В учебном пособии представлены: полный курс лекций по дисциплинам входящим в курс «Прикладная механика» - «Теоретическая механика», «Сопротивление материалов» и «Детали машин» для студентов технологических специальностей, методика проведения лабораторных работ, задания и примеры решения расчетно-графических работ, а также тестовые вопросы к выходному контролю по данным дисциплинам. Пособие предназначено для студентов очной и заочной форм обучения для подготовки к сдаче рубежных и выходного контролей.

УДК 539.3/.6(075,8)

ББК 30.121.73

ISBN © Скотников Д.А., 2011

© Анисимов А.В., 2011

© Марьина А.А., 2011

ЧАСТЬ ПЕРВАЯ

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

Основные понятия.

Теоретическая механика – это наука, изучающая взаимодействие материальных тел и их поведение в результате этого взаимодействия.

Принято различать два основных состояния материальных тел: покой и движение.

Состояние покоя – сохранение каждой точкой тела своего положения в выбранной системе координат с течением времени.

Состояние движения – изменение каждой точкой тела своего положения в выбранной системе координат с течением времени. Состояния покоя и движения относительны, поскольку тело может покоиться в выбранной системе координат, но двигаться вместе с системой.

Механическим движением называется изменение с течением времени взаимного положения материальных тел или их частей в пространстве.

Теоретическую механику принято делить на три основных раздела: статику, кинематику и динамику.

Статика – это раздел теоретической механики, изучающий условия сохранения материальными телами состояния покоя, или другими словами, изучает равновесие тел под действием сил.

Кинематика изучает движение материальных тел, без учета действующих на них сил и их инертности, а также основные характеристики движения тел и взаимосвязь этих характеристик.

Динамика изучает движение материальных тел под действием сил.

Статика

1.1.1. Понятия и определения. Аксиомы статики

Основная задача статики – изучение условий равновесия тел.

Силой в теоретической механике называют величину, являющуюся количественной мерой взаимодействия материальных тел.

Сила характеризуется тремя величинами:

- численным значением (модулем);

- направлением действия;

- точкой приложения.

Система сил – вся совокупность сил, принятых к рассмотрению и действующих на рассматриваемую систему тел.

Внешними называются такие силы, которые действуют на рассматриваемое тело со стороны других материальных тел.

Внутренними называют силы, которые возникают только от действия частиц одного и того же тела.

По характеру действия силы различают:

1) Сосредоточенные – действующие в точке.

2) Распределенные – действующие на определенной длине.

3) Поверхностные – действующие по некоторой площади.

АКСИОМА №1. (закон действия и противодействия). Две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны.

Эта аксиома предполагает дальнодействие, т. е. возможность действия материальных тел друг на друга на расстоянии, что характерно для классической механики.

Если точка А с массой m_А действует на точку В с силой F _B, а точка В с массой m_В действует на точку А с силой F _A (рис.1.1), причем точки А и В получают от действия этих сил ускорения, соответственно равные а_A и а_В то имеем: F_B = -F_A и F_A = F_B или m_А·а_А=m_В·а_В ; следовательно, ускорения, сообщаемые материальным точкам силами взаимодействия, обратно пропорциональны массам точек.

АКСИОМА №2 (закон независимости действия сил). Если на материальную точку действует одновременно несколько сил, то каждая из этих сил действует независимо от других и сообщает точке ускорение, равное этой силе, деленной на массу точки. Следовательно, система нескольких сил F₁, F_2,… F_n действует на материальную точку так же, как одна сила F, равная сумме F₁, F_2,… F_n, т. е.

, (1.1)

Это следствие представляет обобщенный закон параллелограмма сил.

АКСИОМА №3 Твердое тело находится в равновесии под действием двух сил только в том случае, если эти силы равны по модулю и направлены в противоположные стороны по общей линии действия (рис. 1.2).

Эти две силы называются уравновешивающимися. Силы называются уравновешивающимися, если твердое тело, к которому приложены эти силы, находится в состоянии покоя.

АКСИОМА №4 Не нарушая состояния твердого тела, можно добавлять и отбрасывать уравновешенные системы сил.

Следствие: не нарушая состояния твердого тела, силу можно переносить по ее линии действия в любую точку тела.

Две системы сил называются эквивалентными, если одну из них можно заменить другой, не нарушая состояния твердого тела.

Равнодействующей называется сила, которая эквивалентна данной системе сил.

АКСИОМА №5 Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке, равна по модулю диагонали параллелограмма, построенного на этих силах, и направлена вдоль этой диагонали (рис. 1.3).

По модулю равнодействующая равна:

R= , (1.2)

Система сил – вся совокупность сил, принятых к рассмотрению и действующих на рассматриваемую систему тел.

Линия действия вектора силы – бесконечная прямая, проходящая через данный вектор.

Эквивалентные системы сил – это такие системы сил, воздействие которых на данную систему тел приводит к одному и тому же поведению этих тел.

Уравновешенная система сил - это такая система сил, действие которой на данную систему тел эквивалентно отсутствию всякого действия (т.е. действие равно нулю).

Связанный вектор - вектор, приложенный к определенной точке пространства и не допускающий переноса в другие точки.

Скользящий вектор - вектор, который можно располагать в любой точке на линии его действия.

Свободный вектор - вектор, который можно располагать в любой точке пространства.

Абсолютно твердое (жесткое) тело - материальное тело, деформациями которого в процессе его нагружения или взаимодействия с другими телами мы пренебрегаем (тело сохраняет свою форму).

1.1.2. Связи

Если каждая из точек системы может занимать произвольное положение в пространстве и иметь произвольные скорости, то система называется свободной.

Условия, которые налагают ограничения на движение системы, называются связями.

Так, для лампы, подвешенной на шнуре, связью является шнур; для книги, лежащей па столе, связью является стол; для лестницы, приставленной к стене, связями являются пол и стена. Для шара, катящегося по бильярдному столу, связью является поверхность стола и его борта.

Реакция - это сила взаимодействия опоры и рассматриваемого тела.

Свободное тело - такое материальное тело, которое не связано с другими материальными телами и которому из данного положения можно сообщить любое перемещение в пространстве.

Сила, с которой тело действует на связь, называется силой давления.

Сила, с которой связь действует на тело, препятствуя его перемещению, называется силой реакции.

Сила, давления и сила реакции связи по модулю равны и действуют по одной прямой в противоположные стороны.

Методика определения реакций связей при решении задач статики:

1. Несвободное тело условно изображают как свободное с помощью принципа освобождаемости – всякое несвободное тело можно рассматривать как свободное, если отбросить связи и заменить их реакциями связей.

2. В результате применения этого принципа мы получаем тело свободное от связей и находящееся под действием некоторой системы сил.

3. Направление реакции связи противоположно направлению перемещения, уничтожаемого данной связью.

1.1.3. Основные виды связей и их реакции

1) Абсолютно гладкая поверхность.

Реакция всегда направлена перпендикулярно поверхности контакта (рис. 1.4).

Примечание. Если поверхность криволинейна, то реакция всегда направлена перпендикулярно касательной к поверхности.

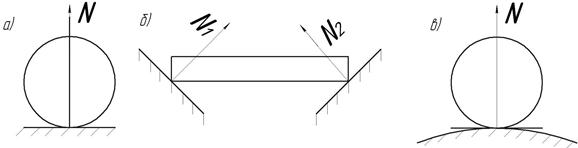
Рис.1.4

2) Шероховатая поверхность.

Реакция имеет две составляющие - одну перпендикулярно поверхности контакта (нормальная реакция) и другую вдоль поверхности контакта (сила трения) (рис. 1.5)

Рис. 1.5

Стержень - тело, способное выдерживать как сжимающую, так и растягивающую нагрузку.

Нить - тело, способное выдерживать только растягивающую нагрузку.

Балка - тело, способное выдерживать растягивающую, сжимающую и изгибающую нагрузки.

3) Стержень (нить).

Реакция всегда направлена вдоль стержня или нити (рис. 1.6).

Рис. 1.6

4) Подвижный шарнир.

Шарнир - это такое соединение двух жестких тел, при котором тела не могут разъединиться, но могут поворачиваться друг относительно друга. Реакция направлена перпендикулярно опорной поверхности (рис. 1.7).

Рис.1.7

5) Неподвижный шарнир.

Реакции две и направлены они так, чтобы не лежать на одной прямой (рис. 1.8).

Рис.1.8

6) Жёсткая заделка.

Две реакции и один реактивный момент (рис. 1.9).

Рис.1.9

1.1.4. Плоская система сходящих сил

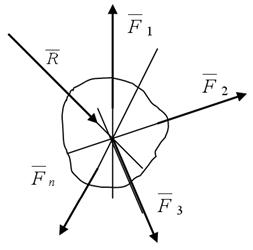Сходящиеся силы- это силы, линии, действия которых пересекаются в одной точке. Пусть на тело действует система сходящихся сил ₁… _n, то есть сил, линии действия которых сходятся в одной точке (рис. 1.10). Такая система сил будет иметь главный вектор , приложенный в точке пересечения их линий действия и определяемый аналитически по формуле:

. (1.3)

Рис.1.10

Различают плоскую систему сходящихся сил – когда линии действия всех данных сил лежат в одной плоскости и пространственную, когда линии действия лежат в различных плоскостях.

Кроме аналитического способа нахождения главного вектора существует геометрический способ называемый
правилом многоугольника (рис.1.11). Он заключается в следующем: в масштабе согласно (рис.1.10) откладывается величина вектора ₁, из его конца откладывается величина вектора ₂ под углом образованным силами ₁ и ₂, далее аналогично

Рис.1.11 откладываются силы ₃ и _n. Конец последней слагаемой силы соединяется с началом первой главным вектором R. Результирующий (главный) вектор направлен из начала F₁ к концу F_n.

Вывод: система сходящихся сил имеет равнодействующую равную геометрической сумме этих сил, приложенную в точке пересечения их линий действия.

Уравнение равновесия плоской системы сходящихся сил: плоская система сходящихся сил находится в равновесии, когда алгебраическая сумма проекций сил на каждую из двух координатных осей равна 0.

(1.4)

Или когда геометрическая сумма всех сил системы равна 0 или , т.е. когда силовой многоугольник замкнут.

Закон параллелограмма сил – 2 силы, приложенные в одной точке, имеют равнодействующую (главный вектор) приложенную в этой точке (рис.1.12).

Рис.1.12 R = . (1.5)

1.1.5. Проекции силы на координатную ось

Проекция силы на ось есть скалярная величина равная произведению модуля силы на косинус угла между силой и положительным направлением оси (рис.1. 13).

Рис.1.13 F_x = F·cosα = AB. (1.6)

Частные случаи проекции силы на оси координат.

а) б) в)

Рис.1.14

Если сила ₁ перпендикулярна оси х (рис.1.14 а), то ее проекция на ось х равна F_1x = 0; если сила ₂ находится под углом α к оси х (рис. 1.14 б), то ее проекция равна F_2x =F₂ cosα; если сила ₃ лежит на оси х и ее направление совпадает с направлением оси (рис. 1.14 в), то проекция равна F_3x = F₃.

1.1.6. Момент силы относительно точки (центра)

Моментом силы М относительно центра О называется вектор, модуль которого равен произведению силы F на плечо h (рис.13)

M=F·h, (1.7)

где h – плечо, кратчайшее расстояние (перпендикуляр)

Рис.1.15 от линии действия силы до выбранной точки.

В дальнейшем будем руководствоваться следующим правилом определения знака момента: момент считается положительным, если сила пытается повернуть конструкцию относительно центра момента против хода часовой стрелки.

Два вектора называются коллинеарными, если их линии действия параллельны.

Теорема Вариньона: сумма моментов сил относительно выбранной точки (центра) равна моменту равнодействующей этих сил относительно той же точки.

, (1.8)

1.1.7. Условия равновесия произвольной плоской системы сил

Первое условие

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы проекции всех сил на каждую из двух координатных осей, и сумма их моментов относительного любого центра, лежащего в плоскости действия сил, были равны нулю.

∑ F_ix=0

∑ F_iy=0, (1.9)

∑ М_о=0

где ∑М_о – сумма моментов относительно точки О.

Второе условие

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно каких-либо центров А и В и сумма проекций сил на ось х (не перпендикулярную к прямой АВ) были равны нулю.

∑ М_А=0

∑М_В=0, (1.10)

∑F_ix=0

Третье условие

Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы суммы моментов всех этих сил относительно любых центров А,В,С не лежащих на одной прямой были равны нулю.

∑М_А=0

∑М_В=0 (1.11)

∑М_С=0

Задача статики может быть решена только в том случае, когда для нее число неизвестных реакций связей не превышает числа уравнений равновесия, которые содержат эти неизвестные реакции. Такие задачи называются статически определимыми, а системы тел в этих задачах называют статически определимыми системами.

1.1.8. Пара сил

Парой сил называют две силы, равные по модулю, противоположные по направлению и лежащие на параллельных прямых (рис. 1.16).

Расстояние между линиями действия сил есть плечо пары сил.

Момент пары сил - это сумма моментов каждой из сил составляющих пару.

Две пары сил будут эквивалентными, если равны их моменты.

Рис. 1.16

Теорема. Момент пары сил есть величина постоянная и равная моменту одной из сил, составляющих пару, относительно любой точки, лежащей на линии действия другой силы.

, (1.12)

Правило знаков: условимся считать момент пары положительным, если он стремится вращать тело против хода часовой стрелки.

Свойства пар сил:

1. Пару сил можно свободно перемещать и поворачивать в плоскости ее действия.

2. Пару сил можно переносить из данной плоскости в любую другую плоскость твердого тела, сохраняя параллельность плоскостей действия пар.

3. Пару сил всегда можно заменить другой парой сил, изменив обратно пропорционально расстояние между силами.

4. Две пары называются эквивалентными, если одну из них можно заменить другой, не изменяя состояния тела.

1.1.9. Условие равновесия произвольной плоской системы сил

Теорема (лемма Пуансо). Силу, действующую на данное тело можно переносить параллельно самой себе в любую точку тела, добавляя при этом пару сил с моментом, равным моменту исходной силы относительно новой точки ее приложения.

Доказательство: рассмотрим силу , действующую на тело в точке А (рис. 1.17.а). Добавим в некоторой другой точке тела, например в точке В, две силы и , такие, что и линии действия сил параллельны (рис. 1.17.б). Очевидно, что и представляют собой уравновешенную систему сил и, следовательно, состояние покоя тела не нарушится. Но силы и образуют пару сил и мы получаем систему, у которой имеется сила , приложенная в точке В, и пара сил с некоторым моментом m (рис. 1.17.в), а равновесие тела сохраняется, ч. т. д.

Рис. 1.17

Главный вектор - это сумма всех сил, действующих на рассматриваемую систему тел.

Главный момент системы относительно центра - это сумма моментов всех сил, действующих на рассматриваемую систему тел, относительно выбранного центра.

Теорема о приведении сил к данному центру: Любую плоскую систему сил, действующих на данное тело, можно свести к действию одной силы (главный вектор системы), приложенной в любой выбранной точке тела, и одной пары сил (главный вектор системы).

Доказательство: рассмотрим тело, на которое действует произвольная система сил , ,…, и пары сил с моментами , ,…, (рис. 1.18. а). Выбираем любую точку этого тела, например точку О. Перенесем все силы в эту точку. Согласно лемме Пуансо, при этом необходимо добавить соответствующее количество пар сил с моментами , ,…, (рис. 1.18. б). Поскольку все силы собраны теперь в одной точке, их можно векторно сложить. В результате получим главный вектор системы:

, (1.13)

Также, используя свойства пар сил, можем сложить все действующие моменты пар сил и получить главный момент (рис. 1.18. в):

, (1.14)

Рис.1.18

Плоская система произвольно расположенных сил находится в равновесии, когда главный момент и главный вектор равны 0:

, (1.15)

Это означает, что силовой многоугольник, построенный на силах данной системы должен быть замкнутым, следовательно, и алгебраическая сумма проекций сил на каждую из двух координатных осей x и y должна быть равна 0.

Это выражение означает, что алгебраическая сумма моментов сил данной системы относительно любого центра приведения равна 0.

Вывод: для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на оси координат x и y равнялись 0 и чтобы алгебраическая сумма моментов этих сил относительно любой точки плоскости также равнялись 0.

1.1.10. Система параллельных сил

Система сил, линии действия которых параллельны, называется системой параллельных сил.

Теорема: Система параллельных сил всегда имеет равнодействующую.

Равнодействующая приложена к определенной точке, называемой центром параллельных сил.

Координата центра параллельных сил.

Рассмотрим систему , ,..., параллельных сил (рис. 1.19). Заметим, что силы могут быть направлены и в противоположные стороны. Выберем систему координат таким образом, чтобы одна из осей (ось X ) была перпендикулярна линиям действия этих сил.

Рис. 1.19

Определим суммарный момент этих сил относительно начала координат (в приводимой формуле оперируем величинами сил):

. (1.16)

Но на основании теоремы о параллельных силах, мы знаем, что эти силы имеют равнодействующую, поэтому, согласно теореме Вариньона, этот момент должен быть равен моменту равнодействующей относительно начала координат:

, (1.17)

следовательно, приравняв эти моменты, получим

, (1.18)

По другим осям координат выражение получится точно таким же, только в правой части надо соответственно заменить х на у или z. Следовательно, можем записать полученную зависимость в векторной форме:

, (1.19)

Поиск по сайту: