Зубчатые передачи

Принцип действия зубчатой передачи основан на зацеплении зубчатой пары.

Меньшее зубчатое колесо, вращающееся с большей частотой вращения и имеющее меньшее число зубьев, называется шестерней. Ведомое зубчатое колесо, имеющее большее число зубьев и меньшую частоту вращения называется колесом.

Преимущества зубчатых передач: 1) возможность передачи практически любой мощности при широком диапазоне скоростей, 2) компактность, 3) надежность, 4) постоянство передаточного числа, 5) высокий КПД, 6) возможность изготовления из разнообразных материалов.

Недостатки: 1) ограниченность передаточного числа передачи, до 12,5, 2) относительная сложность изготовления, 3) при неточном изготовлении зубчатая передача является источником вибрации и шума.

3.12.1. Классификация зубчатых передач

1) По расположению осей валов – с параллельными, пересекающимися и скрещивающимися осями валов. 2) По форме зубчатого колеса – цилиндрические, конические, эллиптические 3) По форме зуба – прямозубые, косозубые, с круговыми зубьями, шевронные, 4) По взаимному расположению зубчатых колес – с внешним зацеплением и внутренним, 5) По форме профиля зуба – эвольвентные, циклоидальные, передачи Новикова – с круговым профилем зубьев.

Зубчатые передачи могут быть открытыми и закрытыми, силовыми и кинематическими, простыми и планетарными.

Способы изготовления зубчатых колес: литьем, накаткой зубьев на заготовке, нарезание зубьев на заготовке.

3.12.2. Геометрия эвольвентного зубчатого зацепления

Постоянное передаточное отношение зубчатой передачи достигается при определенной форме профиля зубьев. Наибольшее распространение получили эвольвентные профили зубьев. Эвольвентное зацепление обеспечивает высокую прочность зубьев, допускает некоторое изменение межцентрового расстояния при износе или погрешности изготовления.

Эвольвентой называется кривая, описываемая какой – либо точкой, лежащей на прямой, перекатываемой по окружности без скольжения (Рис. 3.24).

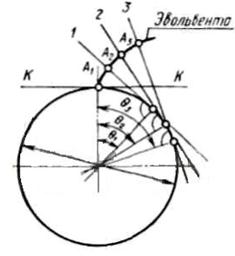
Рис. 3.24. Эвольвентное зацепление

3.12.3. Основные геометрические параметры зубчатой передачи

Основные геометрические параметры зубчатой передачи (Рис. 3.25): межосевое расстояние а_w, число зубьев шестерни z ₁ и колеса z ₂, модуль m, передаточное число U = i.

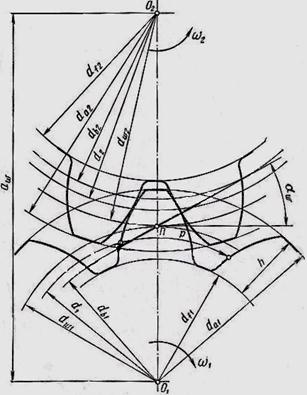
Рис. 3.25. Геометрические параметры зубчатой передачи

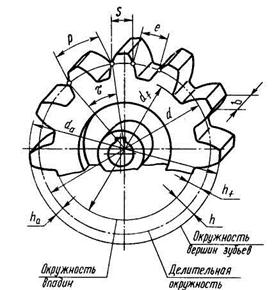Основные геометрические параметры зубчатого колеса (Рис. 3.26): модуль, диаметр делительной окружности d, впадин d_f, вершин d_a, основной d_B, ширина b, высота зуба h_а, число зубьев z.

Рис. 3.26. Геометрические параметры зубчатого колеса

Расстояние между одноименными профилями соседних зубьев по дуге окружности называется окружным шагом P_t.

Линейная величина в π раз меньше окружного шага зубьев называется окружным модулем зубчатого колеса.

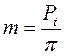. (3.49)

Все размеры зубьев цилиндрических зубчатых колес вычисляют по делительному нормальному модулю, который называется расчетным модулем зубчатого колеса или просто модулем. Значения модулей принимают по ГОСТу

Для цилиндрической прямозубой передачи существуют следующие зависимости:

- модуль – показывает сколько миллиметров делительной окружности зубчатого колеса приходится на 1 зуб:

. (3.50)

межосевое расстояние:

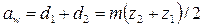. (3.51)

высота зуба:

. (3.52)

где h_a и c – соответственно коэффициенты высоты зуба и коэффициент

радиального зазора, в общем случае их принимают равными h_a=1, с=0,25.

диаметр окружности впадин:

. (3.53)

диаметр окружности впадин:

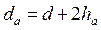. (3.54)

3.12.4. Элементы конструкции зубчатого колеса

1. Венец – часть ЗК, где расположены все зубья

2. Обод – часть ЗК, находящаяся между венцом и ступицей, служит для передачи крутящего момента от зубчатого венца к ступице.

3. Ступица – центральная часть зубчатого колеса с отверстием под вал, служит для соединения колеса с валом. (Рис. 3.27).

Рис. 3.27. Элементы конструкции зубчатого колеса

3.12.5. Материалы зубчатого колеса

Чугунные ЗК – СЧ 21….30.

Стальные ЗК – Ст.3…40, Сталь 40Х, 40ХН, 20ХГСА. Для повышения нагрузочной способности ЗК из углеродистой стали подвергают термообработке – улучшению, нормализации и поверхностной обработке – азотированию, закалке, цементации.

3.12.6. Силы, действующие зацеплении прямозубой цилиндрической передачи

Силовое взаимодействие колес заключается в передаче по линии NN силы нормального давления F_n. Р – полюс; NN – нормаль зацепления (линия давления); α - угол зацепления; F_t - окружная сила (Рис. 3.28).

Рис. 3.28. Схема сил

Окружная сила:

F_t = F_nּcos α. (3.55)

Радиальная сила:

F_r = F_nּsin α. (3.56)

3.12.7. Виды разрушения зубьев

Контактные напряжения сосредотачиваются в пятне контакта и вызывают усталостное выкрашивание поверхности зубьев (в). Напряжения в зубьях возникающие в результате действия изгибающего момента вызывают поломку зубьев у основания (а, б). Кроме усталостных видов разрушения возникает также износ зубьев связанный с недостаточной смазкой и действием абразивных частиц (г), а также заедание зубьев, возникающее при отсутствии смазки или ее выдавливании с поверхности зубьев при действии больших нагрузок (д) (Рис. 3.29). При заедании происходит условное сваривание поверхностей и отрыв поверхностных слоев зубьев зубчатой передачи.

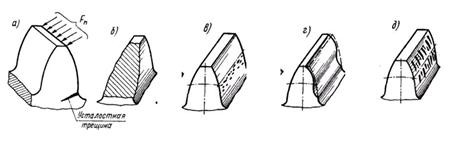
Рис. 3.29.Виды разрушения зубьев

3.12.8. Расчеты на прочность

1. Проверка зубьев колес по контактным напряжениям σ_H, Н/мм²:

, (3.57)

где К – вспомогательный коэффициент,

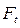- окружная сила в зацеплении, Н;

К_Hα – коэффициент, учитывающий распределение нагрузки между зубьями,

для прямозубых колес К_Hα= 1;

К_Нβ – коэффициент неравномерности нагрузки по длине зуба,

для прирабатывающихся зубьев К_Нβ =1;

К_Hv – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи,

u_ф – фактическое передаточное число.

2. Проверка по напряжениям изгиба зубьев шестерни σ_F1 и колеса σ_F2, Н/мм²:

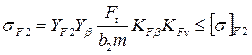, (3.58)

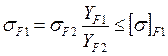. (3.59)

где К_Fα – коэффициент, учитывающий распределение нагрузки между зубьями,

для прямозубых колес К_Fα =1;

К_Fβ – коэффициент неравномерности нагрузки по длине зуба,

для прирабатывающих зубьев колес К_Fβ =1;

К_Fv – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи;

Y_F1 и Y_F2 – коэффициенты формы зуба шестерни и колеса определяются в

зависимости от эквивалентного числа зубьев шестерни и колеса;

Y_β – коэффициент, учитывающий наклон зуба, для прямозубых колес Y_β =1.

Поиск по сайту: