 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Теоретическая часть. 39. 2. 1 Измерения. Основные понятия и постулаты
39. 2. 1 Измерения. Основные понятия и постулаты
Измерения – сложный процесс, включающий в себя взаимодействие целого ряда его структурных элементов. К ним относятся:
- измерительная задача;
- объект измерения;
- принцип, метод и средство измерения и его модель;
- условия измерения;
- субъект измерения;
- результат и погрешность измерения;
Начальным элементом каждого измерения является его задача (цель). Задача любого измерения заключается определении значения выбранной (измеряемой) физической величины с требуемой точностью в данных условиях. Объект измерения – это реальный физический объект, свойства которого характеризуются одной или несколькими измеряемыми физическими величинами.
Метод измерения – это совокупность физических принципов, на которых основаны измерения, например, применение эффекта Джозефсона для измерения электрического напряжения или эффекта Доплера для измерения скорости.
Метод измерения – это прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерения. Метод измерения должен по возможности иметь минимальную погрешность и способствовать исключению систематических погрешностей или переводу их в разряд случайных.
Правильность измерений – это характеристика измерений, отражающая близость к нулю систематических погрешностей результатов измерений.
Субъект измерения – человек.
39.2.2 Постулаты теории измерений
Как и любая другая наука, метрология строится на основе ряда основополагающих постулатов, описывающих ее.
Первым постулатом метрологии является постулат α: в рамках принятой модели объекта исследования существует определенная измеряемая физическая величина и ее истинное значение. Если, например, считать, что деталь представляет собой цилиндр (модель – цилиндр), то она имеет диаметр, который может быть измерен.
Так как при различных целях исследований данному объекту могут быть сопоставлены различные модели, то из постулата α вытекает следствие α1: для данной физической величины объекта измерения существует множество измеряемых величин.
Постулат β: истинное значение измеряемой величины постоянно. Следствие β1: для измерения переменной физической величины необходимо определить ее постоянный параметр – измеряемую величину.
Постулат γ: существует несоответствие измеряемой величины исследуемому свойству объекта (пороговое несоответствие измеряемой величины) пороговое несоответствие принципиально ограничивает достижимую точность измерений при принятом определении измеряемой физической величины. Следствие γ1: истинное значение измеряемой величины отыскать невозможно. Следствие γ2: достижимая точность измерения определяется априорной информацией об объекте измерения.
39..2. 3 Сведения о средстве измерения
Понятие «средство измерения» является одним из важнейших в теоретической метрологии. РМГ 29 - 99 определяет средство измерения как техническое средство, используемое при измерениях и имеющее нормированные метрологические свойства.
Средство измерения содержит устройства (блоки, модули), которые выполняют эти элементарные операции. Такие устройства называются элементарными средствами измерений. В их число входят измерительные преобразователи, меры и устройства сравнения.
Измерительный преобразователь – это техническое устройство, построенное на определенном физическом принципе и выполняющее одно частное измерительное преобразование, т.е. операцию преобразования входного сигнала X в выходной X1, информативный параметр которого с заданной степенью точности функционально связан с информативным параметром входного сигнала и может быть измерен с достаточной степенью точности.
Мера – это средство измерений, предназначенное для воспроизведения и хранения физической величины одного (однозначная мера) или нескольких (многозначная мера) размеров, значение которых выражены в установленных единицах и известны с необходимой точностью.
Устройство сравнения (компаратор) – это средство измерений, дающее возможность выполнять сравнение мер однородных величин или же показаний измерительных приборов.
Средства измерений, используемые в различных областях науки и техники, чрезвычайно многообразны. Однако для этого множества можно выделить некоторые общие признаки, присущие всем средствам измерений независимо от области применения.
По роли, выполняемой в системе обеспечения единства измерений, средства измерений делятся на:
- метрологические, предназначенные для воспроизведения единицы и ее хранения или передачи размера единицы рабочим средствам измерений;
- рабочие, применяемые для измерений, не связанных с передачей размера единиц.
Подавляющее большинство используемых на практике средств измерений принадлежат ко второй группе. Метрологические средства измерений весьма немногочисленны. Они разрабатываются, производятся и эксплуатируются в специализированных научно-исследовательских центрах.
По уровню автоматизации все средства измерений делятся на:
- неавтоматические;
- автоматизированные, производящие в автоматизированном режиме одну или часть измерительной операции;
- автоматические, производящие в автоматическом режиме измерения и все операции, связанные с обработкой их результатов, регистрацией, передачей данных или выработкой управляющих сигналов.
В настоящее время все большее распространение получают автоматизированные и автоматические средства измерений. Это связано с широким использованием в средствах измерений электронной и микропроцессорной техники.
По уровню стандартизации средства измерений подразделяются на:
- стандартизованные, изготовленные в соответствии с требованиями государственного или отраслевого стандарта;
- нестандартизированные, предназначенные ля решения специальной измерительной задачи, в стандартизации требований в которых нет необходимости.
По отношению к измеряемой физической величине средства измерений делятся на:
- основные это средства измерений той физической величины, значение которой необходимо получить в соответствии с измерительной задачей;
- вспомогательные – это средства измерений той физической величины, влияние которой на основное средство измерений или объект измерения необходимо учесть для получения результатов измерения требуемой точности.
39. 2. 4 Принцип действия ваттметра
Принцип действия ваттметра основан на взаимодействии токов, протекающих по двум рамкам (катушкам), одна из которых подвижная (обмотка напряжения) 2 - 2, включаемая в цепь параллельно.

Рисунок 39. 1 – Схема включения ваттметра
Ток I2 в обмотке напряжения 2 - 2 пропорционален напряжению в контролируемой цепи и совпадает с ним по фазе. Ток совпадает по фазе с напряжением, потому что цепь обмотки напряжения ваттметра обладает практически чисто активным сопротивлением, а ток Ir равен току I нагрузки. Момент, действующий на подвижную обмотку, равен:
Мв р = С U I cos φ = CP, (39. 2)
где С – коэффициент пропорциональности.
Поскольку противодействующий момент Мпр пропорционален углу поворота α стрелки, отклонение стрелки пропорционально измеряемой активной мощности Р.
Для правильного включения ваттметра один из выводов токовой обмотки и дин из выводов обмотки напряжения отмечают звездочками (*). Эти выводы, называемые генераторными, необходимо включать со стороны источника питания.
Ваттметр – прибор, имеющий назначение измерять работу, совершаемую электрическим током в единицу времени при прохождении тока через какой-либо проводник, так, например, ваттметр может дать число ватт, потребных для получения некоторой силы электрического света в каждую секунду каким-либо механизмом, приводимым в движение при посредстве электрического тока и т.д. Работа, совершаемая электрическим током в течение секунды (в ваттах), определяется произведением числа ампер, выражающего силу тока, проходящего через исследуемую часть цепи, на разность потенциалов, выраженную в вольтах, концов этой части цепи. Вследствие этого, различные ваттметры представляют собой в сущности не что иное, как электродинамометр, через одну катушку которого, приготовленную из толстой проволоки и имеющую небольшое числи оборотов ток, а другая катушка этого электродинамометра, имеющая обыкновенно большое число оборотов тонкой проволоки и часто последовательно соединенная с проводником большего сопротивления, вводится, как ветвь, параллельно исследуемой части цепи. Через эту катушку, очевидно, будет проходить ток, по величине пропорциональной разности потенциалов на концах изучаемой в отношении работы тока части цепи. Так как подвижная катушка электродинамометра испытывает вращающее действие, пропорциональное произведению сил токов в обеих катушках, то, в данном случае, это действие будет пропорционально произведению числа ампер – силы тока в данном проводнике на число вольт, выражающее разность потенциалов этого проводника, то есть будет пропорционально числу ватт, доставляемому током исследуемой части цепи. Подвижная катушка удерживается в своем первоначальном положении без отклонения закручиванием нити или пружинки, на которой она подвешена. Опытом определяется значение одного градуса такого кручения и тогда число градусов, на которое во время опыт произведено закручивание, для удержания подвижной катушки в ее первоначальном положении, дает прямо возможность определить число ватт развиваемых током.
39.2.5 Электронный трехфазный ваттметр - счетчик ЦЭ 6802
ТУ 25-7565.010 - 93
Назначение.
Предназначен для измерения активной мощности и электроэнергии в трех- и четырехпроводных, трехфазных и двухпроводных однофазных цепях переменного тока. Для измерения реактивной мощности и энергии в трехфазных цепях переменного тока. Для поверки счетчиков активной электроэнергии класса 0,2иниже, поверки ирегулировки3-хфазных ваттметров и счетчиков реактивной энергии класса 0,5 и ниже. Для измерения величины тока и напряжения по 3-м фазам с точностью класса 0,2. Для проверки амперметров и вольтметров переменного тока класса 0,5 и ниже методом образцового прибора. Измерение величины напряжения и тока по трем фазам с точностью 0,2.
Область применения.
Региональные, территориальные, городские и районные предприятия Гостехнадзора. Органы сертификации электроустановок. Метрологические, ремонтные службы. Предприятия- изготовители средств учета электроэнергии. Контрольно-измерительные лаборатории промышленных предприятий.
Нормативно - правовое обеспечение:
- соответствие ГОСТ 22261 – 94 Средства измерений электрических и магнитных величин. Общие технические условия;
- сертифицированы в Украине и СНГ;
- внесены в Госреестр средств измерений Украины (№13548 - 93).
Особенности:
- одновременная поверка от 1 до 8 счетчиков, имеющих телеметрические выходы;
- автоматизированная обработка информации;
- отображение результатов измерений на цифровом дисплее;
- высокая временная и температурная стабильность;
- возможность работы в составе компьютерных комплексов через интерфейс ИРПС;
- индикация измеренных значений токов и напряжений раздельно по фазам в Вольтах и Амперах;
- контроль частоты измерительных сигналов в Герцах;
- контроль угла сдвига фаз (в градусах), значения cos φ;
- имеет встроенную защиту от перегрузки, не критичен к подаче переменного напряжения до 450 Вт по параллельным цепям.
Характеристики надежности:
- межповерочный интервал - 1 год;
- гарантийный срок эксплуатации - 3 года.
Таблица 39.1 – Технические характеристики электронного трехфазного ваттметра – счетчика ЦЭ 6802
| Класс точности при изменении, Вт: - активной мощности (энергии) - реактивной мощности (энергии) - напряжения переменного тока - силы переменного тока | 0,05 (0,05) 0,1 (0,1) 0,2 0,2 |
| Номинальное значение напряжения, Вт: - фазные - линейные | 57,7; 127; 220; 100; 220; 380 |
| Диапазон напряжений в % от номинального значения | 85-110 |
| Напряжение сети питания, Вт | |
| Частота измерительной сети, Гц | 47,5-63 |
| Номинальная сила тока (Iном), А | 5 или 1 |
| Диапазон токов в % от номинального значения | 1-150 |
| Полная потребляемая мощность, В*А | |
| Количество поверяемых счетчиков | 1-8 |
| Диапазон рабочих температур, °С | от 10 до 40 |
| Габаритные размеры, мм | 450´440´290 |
| Масса, не более, кг |
Счетчики ЦЭ 6802 используется как образцовый в составе установки МК 6801 для поверки и регулировки счетчиков электроэнергии.
39. 2. 6 Погрешности измерения ваттметром
Основными составляющими погрешности измерения ваттметром являются нормируемые в ГОСТ 84 76 – 93 погрешность, вызванная изменением температуры окружающего воздуха, отклонением напряжения от номинального.
ГОСТ 22261 – 94 нормирует погрешность ваттметра при нормальных условиях, а именно (метрологические характеристики):
- при температуре 200С 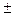 20С;
20С;
- положение любое между горизонтальным и вертикальным 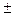 10 рабочей области;
10 рабочей области;
- ориентация прибора относительно магнитного поля земли - любая 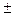 50 от указанного направления ориентации;
50 от указанного направления ориентации;
- частота 45-65 Гц.
Таблица 39. 2 – Пределы допускаемой погрешности
| Класс точности | 0,05 | 0,1 | 0,2 | 0,5 | 1,5 | 2,5 | |||
| Предел допускаемой погрешности | 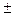 0,05 0,05
| 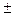 0,1 0,1
| 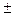 0,2 0,2
| 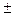 0,5 0,5
| 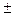 1 1
| 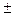 1,5 1,5
| 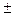 2,5 2,5
| 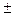 4 4
| 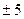
|
Для ваттметра, используемого в данной лабораторной работе, класса точности 0,2 предел допускаемой основной погрешности 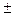 0,2.
0,2.
Предел допускаемой дополнительной погрешности приборов, вызванной изменением температуры окружающего воздуха от нормальной до любой температуры в пределах, установленных рабочими условиями применения, на каждые 10 0С должен быть равен:
- предел допускаемой основной погрешности для приборов соответствующих по климатическим условиям 2 – 4 группам по ГОСТ 22261 – 94;
- 0,8 предела допускаемой основной погрешности - для приборов, соответствующих климатическим условиям 5-й группы по ГОСТ 22261 – 94;
- 0,6 предела допускаемой основной погрешности – для приборов, соответствующих климатическим условиям 6 и 7-й группам по ГОСТ 22261 – 94 классов точности 0,2 и 0,5.
Предел допускаемой дополнительной погрешности, вызванной отклонением напряжения от номинального (57,7; 127; 220 – фазное, 100; 220; 380 – линейное) в пределах рабочей области, при неизменном значении измеряемой мощности нормируется ГОСТ 8476-93 как равный пределу допускаемой основной погрешности (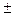 0,2).
0,2).
Суммарная погрешность результата измерений состоит из неисключенной систематической погрешности (НСП) и случайной погрешности.
Вычисляем неисключенную систематическую погрешность по формуле (39.3):
Q(p)= ±| ∑Qi |, (39.3)
Таблица 39.3 – Значения коэффициента K
| n | K(p) |
| 5 и более | 1,45 |
| 1,4 | |
| 1,3 | |
| 1,2 |
Вычисляем среднеквадратическое отклонение по формуле (39.4):
 (39.4)
(39.4)
где хi – результат i-го единичного измерения;
 среднее арифметическое значение измеряемой величины.
среднее арифметическое значение измеряемой величины.
По соотношению между Q(p) и S определяем, по какому из трех случаев будем проводить расчет:
1) если Q(p)/S<0,8, то НСП Θ(p) пренебрегают и принимают случайную погрешность  (р) за погрешность результата измерений (39.5):
(р) за погрешность результата измерений (39.5):
 (р) = S(X)·ZP/2 =
(р) = S(X)·ZP/2 = 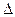 (р), (39.5)
(р), (39.5)
2) если Q(p)/S > 8,то пренебрегают случайной погрешностью и принимают
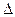 (р) = Θ(p), (39.6)
(р) = Θ(p), (39.6)
3) если  то доверительные границы погрешности результата измерений вычисляют по формуле (39.7):
то доверительные границы погрешности результата измерений вычисляют по формуле (39.7):
 , (39.7)
, (39.7)
K Σ = 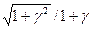 , (39.8)
, (39.8)
 , (39.9)
, (39.9)
где К(Р) = 1,3 согласно таблицы 39.3, если число результатов наблюдений равно 3.
Результат измерения имеет вид:
 , (39.10)
, (39.10)
Поиск по сайту: