 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Динамика поступательного движения
План.
1. Первый закон Ньютона и понятие инерциальной системы отсчёта.
2. Второй закон Ньютона как уравнение движения. Понятие массы, силы, импульса.
3. Третий закон Ньютона и пределы его применения.
4. Неинерциальные системы отсчёта. Абсолютные и относительные скорости и ускорения. Силы инерции (центробежная сила и сила Кориолиса).
5. Центр инерции (центр масс). Теорема о движении центра инерции.
1. 1-ый закон Ньютона. Материальная точка, не подверженная внешним воздействиям, либо находится в покое, либо движется равномерно и прямолинейно. Такое тело называется свободным,его движение – свободным движением или движением по инерции.
Классическая механика постулирует, что существует система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно. Такая система называется инерциальной системой отсчёта. Таким образом, 1-ый закон Ньютона выражает критерий инерциальности системы отсчёта.
2. 2-ой закон Ньютона. Производная импульса материальной точки по времени равна действующей на неё силе.
, где 
- импульс (количество движения).
Импульс механической системы равен геометрической сумме импульсов всех точек системы.
Сила – величина векторная и в каждый момент времени характеризуется численным значением, направлением в пространстве и точкой приложения. Сложение сил производится по правилу параллелограмма. В современной физике различают 4 вида взаимодействий:
1) гравитационное (обусловлено всемирным тяготением);
2) электромагнитное (осуществляется через электрические и магнитные поля);
3) сильное или ядерное (обеспечивающее связь частиц в атомном ядре);
4) слабое (ответственные за многие процессы распада элементарных частиц).
3. 3-ий закон Ньютона. Силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки.
Третий закон, как и 1-ый и 2-ой справедливы лишь в инерциальных системах отсчёта. Кроме того, отступление от 3-го закона наблюдается в случае движения тел со скоростями, сравнимыми со скоростью света.
В случае движущихся зарядов необходимо учитывать также взаимодействие с магнитными полями, создаваемыми ими.
4. Неинерциальные системы отсчёта. Силы инерции.
Две системы отсчёта, из которых К является инерциальной, а система K’ движется относительно К с некоторым ускорением и, следовательно, неинерциальная.
То есть относительно системы K’ частица ведёт себя так, как если бы кроме силы K’ на нее действует дополнительная сила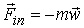 
. Эта сила называется силой инерции.
Движение относительно выбранной условно неподвижной системы называется абсолютным. Вектор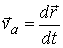 
даёт абсолютную скорость,
абсолютное ускорение, а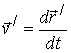 
и 
относительные скорость и ускорение.
где 
единичный вектор, направленный к центру диска. Эта сила называется центробежной силой инерции. Она возникает во вращающихся (неинерциальных) системах отсчёта независимо от того, покоится тело в этой системе или движется относительно неё со скоростью 
.
При движении тела ( 
) в неинерциальной вращающей системе отсчёта, кроме центробежной силы возникает еще одна сила инерции, называемая силой Кориолиса.
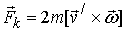- сила Кориолиса, которую можно представить в виде векторного произведения.
5. Центр инерции. Центром инерции (центром масс) системы материальных точек (частиц) называется точка С, положение которой задаётся радиус-вектором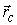 
, определённым следующим образом: 
где 
масса 
ой частицы, 
радиус-вектор, определяющий положение этой частицы, m - масса системы.
В однородном поле сил тяжести центр инерции совпадает с центром тяжести системы.
Поиск по сайту: