АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Кинематика поступательного движения

Читайте также:
  1. А — при двустороннем движении судов; б — при одностороннем движения
  2. Анализ движения дебиторской и кредиторской задолженности
  3. Анализ движения денежной наличности
  4. Анализ движения денежных средств
  5. Анализ движения денежных средств прямым и косвенным методом
  6. Анализ движения и технического состояния основных средств
  7. Анализ движения основных фондов
  8. Анализ наличия и движения основных средств
  9. Анализ остатков и движения денежной наличности
  10. Анализ причин ДТП и меры, повышающие безопасность движения.
  11. Анализ случаев нарушения безопасности движения с установлением виновных и конкретных нарушений правил и порядка работы
  12. Анализ состояния и движения собственного капитала

МЕХАНИКА

Лекция № 1

План

1. Элементы векторной алгебры и векторного анализа. Определение векторов. Сложение и вычитание векторов. Единичный вектор (орт). Проекция вектора на ось. Модуль вектора. Радиус-вектор. Умножение векторов. Дифференцирование векторных величин.

2. Поступательное движение. Система отсчёта. Принцип относительности Галилея. Преобразования Галилея. Границы применимости классического способа описания движения.

3. Понятие материальной точки. Траектория. Путь и перемещение. Скорость и ускорение, их модули.

4. Радиус кривизны траектории. Тангенциальное и нормальное ускорение.

 

1. Элементы векторной алгебры и векторного анализа.

Векторы – величины, характеризующиеся численным значением, направлением и складывающиеся по правилу параллелограмма.

 

 

= + = +

= +

 

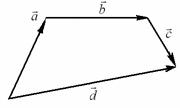
Разностью двух векторов и называется такой вектор , который в сумме с вектором даёт вектор

= -

 

 


 

Всякий вектор можно представить в виде = a * a, где – модуль вектора, а – вектор, называемый единичным вектором или ортом вектора, где а – модуль вектора, a – вектор, называемый единичным вектором или ортом вектора .

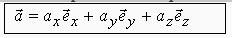Любой вектор можно выразить через его проекции на координатные оси и орты осей.

- модуль любого вектора

Умножение векторов. Скалярное произведение – это скаляр, равный произведению модулей этих векторов на косинус угла между ними.

Скалярное произведение можно выразить через компоненты векторов:

Векторное произведение. Векторным произведением векторов и называется вектор , определяемый формулой:

Векторное произведение можно рассчитать с помощью определителя:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)