Понятие определителя и его свойства

Определитель матрицы второго порядка обозначается и вычисляется так: .

Определение определителя второго порядка. Определитель второго порядка равен разности произведений элементов главной и побочной диагоналей.

Определитель квадратной матрицы третьего порядка определим так:

. (1)

Равенство (1) называют разложением определителя третьего порядка по элементам первой строки. Для более компактной записи такого разложения вводят понятие алгебраического дополнения элемента определителя.

Алгебраическое дополнение элемента определяется равенством

. (2)

Знак алгебраических дополнений, например для определителя третьего порядка в соответствии с первой частью формулы (2) можно символически определить так .

Элемент называется минором элемента определителя и получается вычеркиванием ой строки и го столбца этого определителя. Например,

, .

В результате дополнения будут иметь вид

, .

На основании понятия алгебраического дополнения выражение (1) принимает вид

.

Таким же образом определитель можно разложить по элементам любой строки или любого стлбца.

Например, или .

Совершенно аналогично определяются определители го порядка.

.

Рассмотрим свойства определителей, применение которых часто упрощает процесс вычисления определителей.

Вопрос 6:Свойства определителей
1.При транспонировании матрицы ее определитель не меняется
2.Если в определителе поменять местами две любые строки,два любых столбца,то определитель изменит знак на противоположный
3.Определитель не изменится, если к каждому элементу итой строки прибавит соотвествующий элемент катой строки, умноженный на любое число
4.Определитель равен нулю, если он имеет нулевую строчку или столбец
5.Определитель равен нулю, если он имеет 2 одинаковые строки(два одинаковых столбца)
6.Определитель равен нулю, если он имеет две пропорциональные строки(столбцы)
7.Общий множитель элементов какой-нибудь строки (столбца) можно вынести за знак определителя
8.Определитель равен нулю, если какая-либо из его строк(столбцов) является линейной комбинацией нескольких других строк(столбцов)
Для себя: два столбца умноженные на любое число равны третьему
9.Теорема Лапласа(способ вычисления определителей любых порядков)
Определитель равен сумме произведений элементов любой строки(столбца) на их алгебраическое дополнение

Вопрос 7: Обратная матрица

Вопрос 8: Ранг матрицы

Вопрос 9:не нужно

Вопрос 10:Решение систем линейных уравнений методом Крамера

Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

xi = дельтаi/дельта, где

дельта = det A, а дельтаi – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных

членов bi.

Если система однородна, т.е. bi = 0, то при дельта не равное 0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.

При дельта = 0 система имеет бесконечное множество решений.

Вопрос 11:Матричный метод решения системы линейных уравнений

m=n
A*X=B
X=A^-1*B- формула для решения ур-ий в матричном виде

12.Решение систем линейных уравнений методом Гаусса. Совместные и несовместные системы линейных уравнений

Метод Гаусса (метод исключения известных)

Методом Гаусса можно решать любые совместные системы

Элементарные преобразования системы уравнений
1.Умножение обеих частей ур-ия на число, не равное нулю
2.Прибавление к одному из уравнений системы другого уравнения, умноженного на число, не равное 0.
3.Перестановка местами любые 2 уравнений
4. Вычеркивание одного из пропорциональных или одинаковых уравнений
Две системы уравнений называются эквивалентными, если их решения совпадают
Метод Гаусса- метод решения систем уравнений с помощью элементарных преобразований, осуществляющихся по следующей схеме:
1 туда:
1.Из всех уравнений системы, кроме 1, нужно исключить известное х1
2.Из всех уравнений системы, кроме 1 и 2 исключить неизвестное х2
3. Из всех уравнений системы, кроме 1,2 и 3 исключить неизвестное х3 и т.д.
2 обратно:
1. Из последнего уравнений системы найти хn
2. Представить найденное хn в предпоследнее уравнение системы и найти хn-1
При решении системы методом Гаусса вместо преобразований системы уравнений можно проводить преобразований над строками расширенной матрицы

13.не нужно
14.не нужно

15.не нужно

Вопрос 16:Скалярное произведение векторов.Евклидово пространство

Евкли́довопростра́нство (также Эвкли́довопростра́нство) — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. В этом случае предполагается, что пространство имеет размерность равную 3, т.е. имеется y,x,z

17 и 18 не нужно

Вопрос 19.Прямоугольные координаты на плоскости
Прямоугольная (или декартова) система координат на плоскости задается парой взаимно перпендикулярных координатных осей, имеющих общее начало в точке О и одинаковый масштаб (рис.).

Оси координат на плоскости обычно обозначают Ох и Оу (оси абсцисс и ординат соответственно).

Координатную плоскость обозначают хОу.

Координатные оси делят плоскость хОу на четыре квадранта (или четверти): I, II, III, IV (рис.).

Пусть точка Р лежит на плоскости хОу. Опустим из этой точки перпендикуляры на координатные оси; основания перпендикуляров обозначим P[x] и P[y].

Абсциссой точки Р называется координата х точки P[x] на оси Ох, ординатой — координата у точки P[y] на оси Оу.

Координаты точки обычно указывают в скобках рядом с обозначением точки: Р(х; у).

Между точками на плоскости и парами их координат имеется взаимно однозначное соответствие.

Расстояние между двумя точками и на плоскости определяется с помощью теоремы Пифагора:

Орты осей х, у — это единичные векторы I,j с началом в точке О.

Вопрос 20. Расстояние между двумя точками

Вопрос 21.не нужно

Вопрос 22:Прямоугольная система координат в пространстве. Компланарные вектора.

1.Компланарные вектора(а||в)- векторы, которые лежат на одной прямой или на параллельных прямых.

2.Два вектора называются равными, если они компланарны, одинаково направлены и имеют одинаковую длину.

Свободные векторы- это такие векторы, которые можно переносить
Связные
Компланарные-три вектора в пространстве, если они лежат в одной плоскости или параллельных плоскостях.

Прямоугольная (или декартова) система координат в пространстве задается тройкой попарно перпендикулярных координатных осей, имеющих общее начало в точке О и одинаковый масштаб.

Оси координат в пространстве обычно обозначают Ох, Оу, Оz (оси абсцисс, ординат и аппликат соответственно).

В пространстве возможны правые (рис.)

и левые (рис.)

системы координат; мы будем использовать правую систему координат.

Орты осей Ох, Оу, Оz — это единичные векторы I,j.k с началом в точке О;

направления ортов совпадают с направлением осей.

Орты правой системы координат образуют правую тройку векторов.

Вопрос 23.Условие компланарности 3 векторов

Существует целый ряд условий для трех векторов, который отвечает заихкомпланарность.

Первое условие компланарности именно для трех векторов – это наличие среди трех имеющихся векторов хотя бы одного такого, который был бы нулевым.

Вторым условием является наличие в тройке векторов пары векторов, которые являются компланарными и делают компланарной всю тройку.

Третье условие компланарности логично вытекает из основного, принятым нами за условно базовое определение: линейная зависимость для тройки векторов определяет компланарность этой тройки согласно тому, что компланарность сама по себе и есть такая линейная зависимость.

Вопрос 24.Разложение вектора по 3 некопланарным векторам

Вопрос 25.Прямоугольные координаты точки в пространстве

Координаты векторов и точек в прямоугольной системе координат называются прямоугольными координатами.

Координатами точки A в прямоугольной системе координат называются координаты ее радиус-вектора OA в стандартном базисе. В пространстве это коэффициенты x,y,z в разложении OA=xi+yj+zk, на плоскости — коэффициенты x,y в разложении OA=xi+yj, на прямой — коэффициент x в разложении OA=xi. Прямоугольные координаты точки (или ее радиус-вектора) можно представить координатным столбцом:

в пространстве и на плоскости.

Вопрос 26.Расстояние между двумя точками в пространстве. Проекции ветора на координатные оси.

Расстояние находится по формуле

Проекцией вектора а на координатную ось называют длину отрезка между проекциями начала и конца вектора а (перпендикулярами, опущенными из этих точек на ось) на эту координатную ось.

(Проекцией вектора на координатную ось называют скалярную величину, равную произведению модуля проектируемого вектора на косинус угла между направлениями вектора и выбранной оси).

Проекция вектора, перпендикулярного оси, всегда равна нулю

Проекция вектора, сонаправленного с осью, положительна и равна его модулю, например, sx = s

Проекция вектора, противонаправленного оси, отрицательна и равна его модулю, взятому со знаком «минус», например, sy = –s

Вопрос 27 Условие коллинеарности 2 векторов.

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными.

Два вектора коллинеарные, если отношения их координат равны.

Два вектора коллинеарные, если их векторное произведение равно нулю.

Вопрос 28.Деление отрезка в данном отношении

Вычисление координат некоторой точки С, которая делит заданный отрезок АВ в определенном отношении, может быть выполнено по формулам:

хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ),

где (хА; уА) и (хВ; уВ) – координаты концов заданного отрезка АВ; число λ = АС/СВ – отношение, в котором отрезок АВ делится точкой С, имеющей координаты (хС; уС).

Если отрезок АВ делится точкой С пополам, то число λ = 1 и формулы для хС и уС примут вид:

хС = (хА + хВ)/2, уС = (уА + уВ)/2.

Нужно иметь ввиду, что в задачах λ – это отношение длин отрезков, а поэтому числа, входящие в данное отношение не есть длины самих отрезков в заданной единице измерения. Например, АС = 12 см, СВ = 16 см: λ = АС/СВ = 12 см / 16 см = 3/4.

Вопрос 29.Скалярное произведение 2 векторов и его св-ва. Косинус угла между ними

Вопрос 30.Уравнение прямой на плоскости, проходящей через данную точку перпендикулярно заданному вектору

Вопрос 31.Общее уравнение прямой на плоскости

Вопрос 32.Уравнение прямой с угловым коэфициентом

Вопрос 33:Уравнение прямой на плоскости, проходящей через 2 данные точки

Вопрос 35:Особые случаи общего уравнения прямой на плоскости

Вопрос 36:Угол между двумя прямыми на плоскости (случай, когда прямые заданы уравнениями в общем виде

Угол между двумя прямыми равен углу между их направляющими векторами.

Если прямые заданы следующими уравнениями:

A1x + B1y + C1 = 0 иA2x + B2y + C2 = 0,тогда направляющие векторы этих прямых будут равны:

a1 = (- B1; A1) и a2 = (- B2; A2)

Воспользуемся формулой скалярного произведения двух векторов:

из этой формулы получим:

Выразим угол φ:

Из последней формулы получим:

Вопрос37. Угол между двумя прямыми на плоскости(случай, когда прямые заданы уравнением угловым коэффициентом

Вопрос 38:Условия параллельности и перпендикулярности прямых на плоскости

Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны: 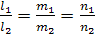– условие параллельности прямых.

Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:

– условие перпендикулярности прямых.

Пример. Найти уравнения прямой проходящей через точку параллельно прямой.

Решение. Поскольку искомая прямая параллельна данной прямой, то в качестве направляющего вектора искомой прямой можно взять направляющий вектор данной прямой.

По условию

– отсюда уравнение искомой прямой имеет вид:. :

Вопрос 39:Расстояние от точки до прямой на плоскости

Вопрос 40:Уравнение плоскости, проходящей через данную точку,перпендикулярно

Заданному направлению

заданному н

Вопрос 41:Уравнение плоскости в отрезках

Вопрос 42: Условие параллельности и перпендикулярности плоскостей

Вопрос 43:Расстояние от точки до плоскости

Вопрос 44:Виды уравнений прямой в пространстве

Вопрос 45: Угол между двумя прямыми. Угол между прямой и плоскостью

Поиск по сайту: