АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Вопрос. Эллипс

Читайте также:
  1. Болгарский вопрос. Соборы на Западе на Востоке. Окончательное разделение 1054 года
  2. Внутренняя политика Екатерины 2. Жалованные грамоты дворянству и городам. Крестьянский вопрос.
  3. Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.
  4. Вопрос.
  5. Вопрос.
  6. Вопрос.
  7. Вопрос.
  8. вопрос.
  9. Вопрос.
  10. Вопрос.
  11. Вопрос. . Что такое наука? Цель науки. Научные знания
  12. Вопрос. Z – преобразование.

Эллипсом называется множество всех точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная больше расстояния между фокусами.

Если оси координат расположены по отношению к эллипсу так, как на рисунке 11, а фокусы эллипса находятся на оси Ох на равных расстояниях от начала координат в точках и , то получится простейшее (каноническое) уравнение эллипса:

. (9)

Здесь а – большая, b – малая полуось, причем а, b и с (с – половина расстояния между фокусами) связаны соотношением .

 

 

 


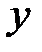
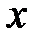
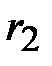
Форма эллипса (мера его сжатия) характеризуется его эксцентриситетом .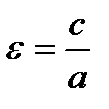

Расстояния некоторой точки эллипса М от его фокусов называются фокальными радиус-векторами этой точки. Их обычно обозначают и . Для любой точки эллипса в силу определения .

Фокальные радиус-векторы выражаются через абсциссу точки эллипса по формулам: (правый фокальный радиус-вектор), (левый фокальный радиус-вектор).

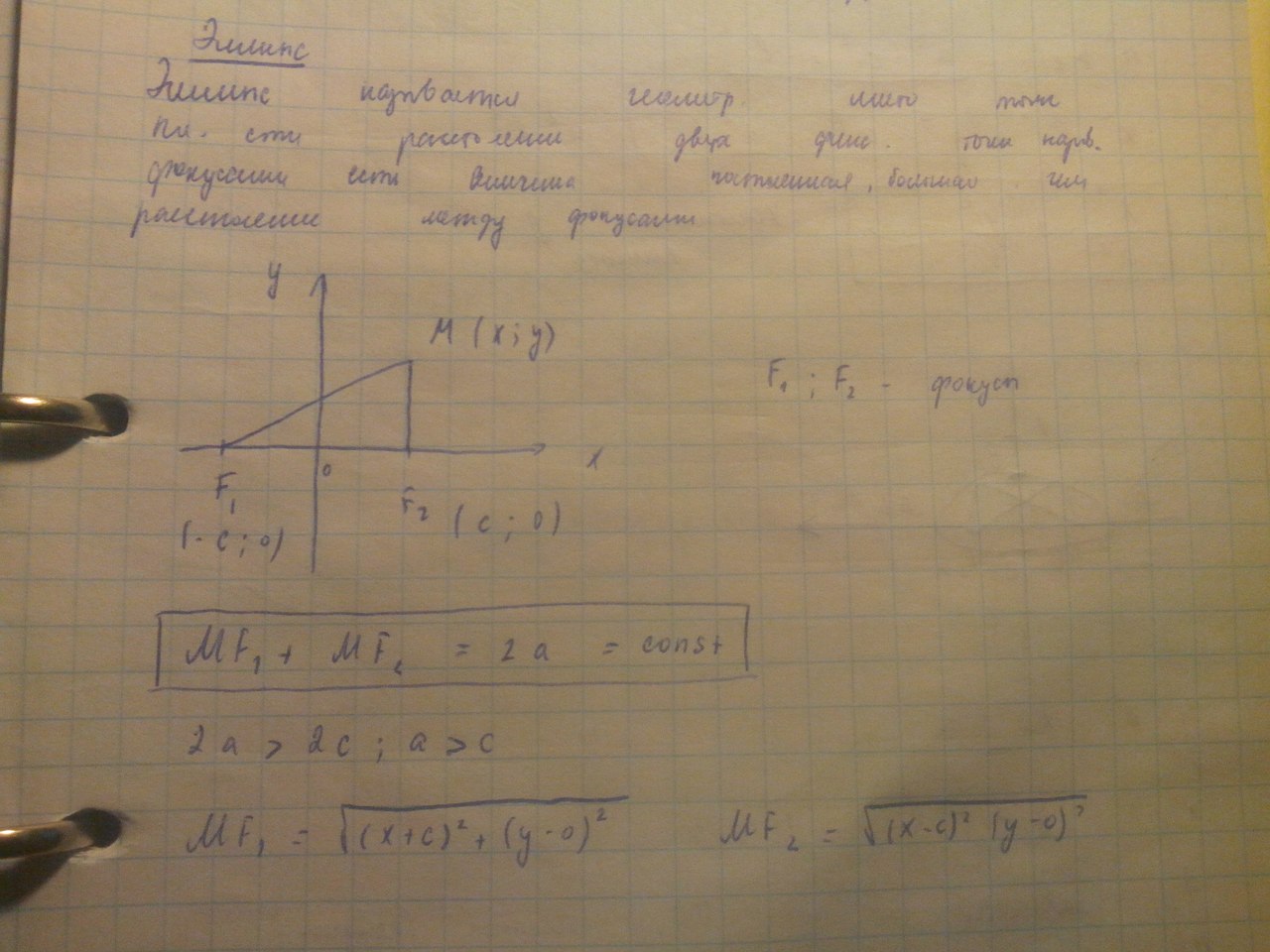
По лекции:


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |

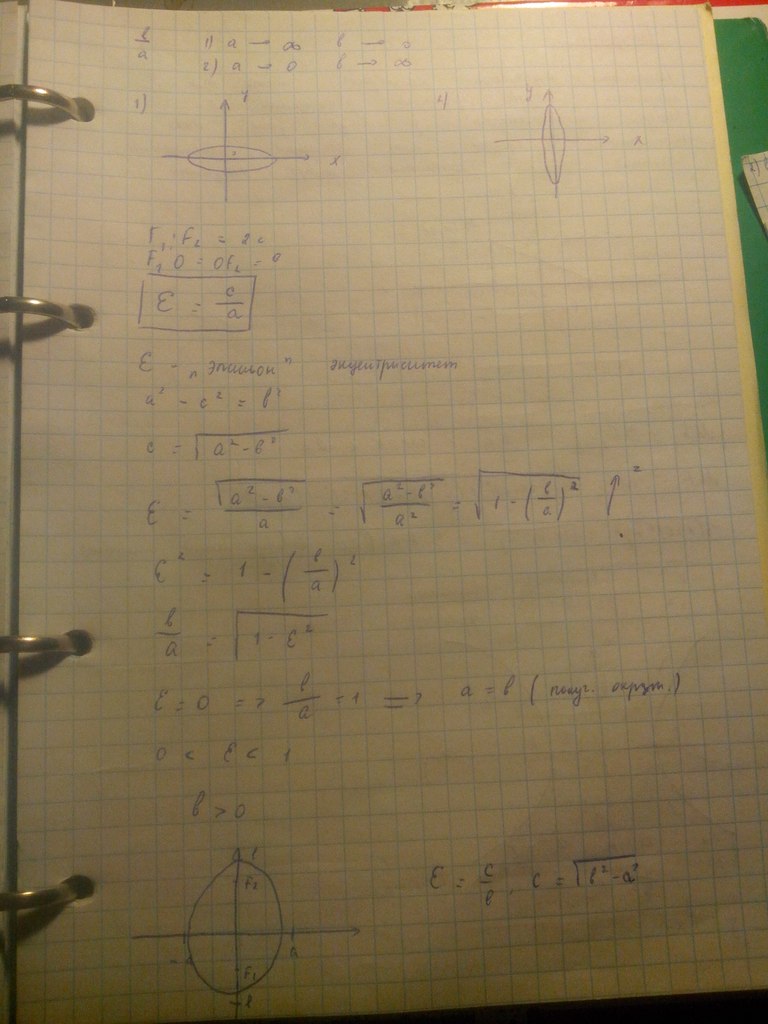
Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)