вопрос. Числовая последовательность

Числовая последовательность — это последовательность элементов числового пространства.

Определение. Пусть X — это либо множество вещественных чисел R, либо множество комплексных чисел C. Тогда последовательность {X_n}^∞_n=1 элементов множества называется числовой последовательностью.

Последовательности. Рассмотрим ряд натуральных чисел:

1, 2, 3, …, n –1, n, ….

Если заменить каждое натуральное число n в этом ряду некоторым числом un, следуя некоторому закону, то мы получим новый ряд чисел: u1, u2, u3, …, un - 1, un, …, кратко обозначаемый { un }

и называемый числовой последовательностью. Величина un называется общим членом последовательности. Обычно числовая последовательность задаётся некоторой формулой un = f (n), позволяющей найти любой член последовательности по его номеру n; эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задаётся путём описания её членов (см. ниже последний пример).

П р и м е р ы числовых последовательностей:

1, 2, 3, 4, 5, … - ряд натуральных чисел;

2, 4, 6, 8, 10, … - ряд чётных чисел

1.4, 1.41, 1.414, 1.4142, … - числовая последовательность

приближённых значений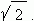

с увеличивающейся точностью.

В последнем примере невозможно дать формулу общего члена последовательности, тем не менее эта последовательность описана полностью.

Вопрос 55: Предел последовательности

Вопрос 56:Бесконечно малые последовательности. Сумма и произведение бесконечно малых

последовательностей

Вопрос 57:Основные теоремы о пределах числовых последовательностей.

Вопрос 58:

Бесконечно большие последовательности

Вопрос 59:Число е

математическая константа, основание натурального логарифма, иррациональное и трансцендентное число. e = 2,718281828459045… Иногда число e называют числом Эйлера или неперовым числом. Играет важную роль в дифференциальном и интегральном исчислении.

трансцендентное (иррациональное, непредставимое в виде комбинации степеней рациональных чисел) число; принятое за основание натуральных логарифмов.

график функции "е в степени х" называется экспонентой, а производная этой функции равна самой функции. эта функция неплохо описывает множество процессов в живой и неживой природе (размножение микроорганизмов, ядерный распад и тд).

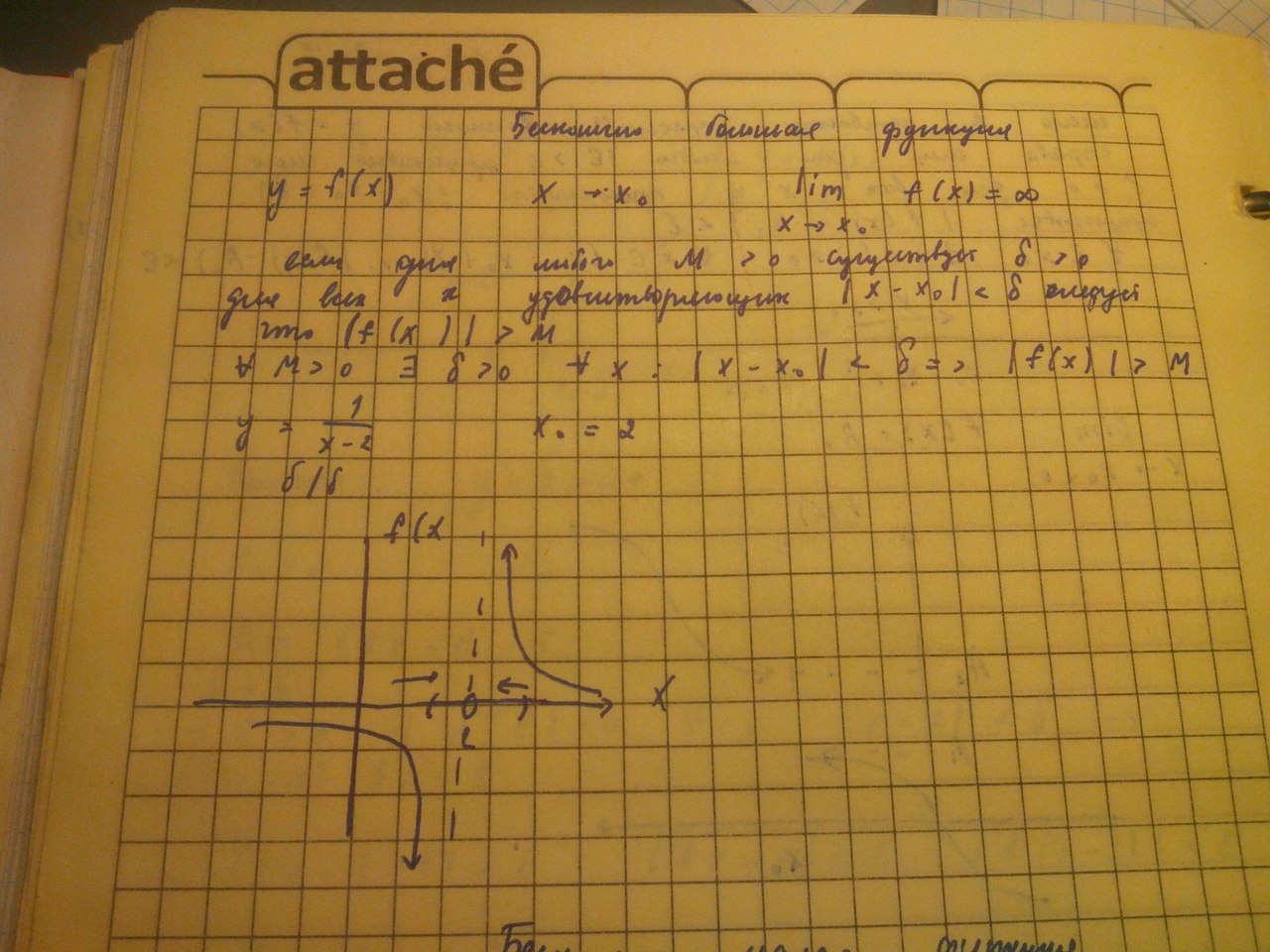
Вопрос 60:Предел функции

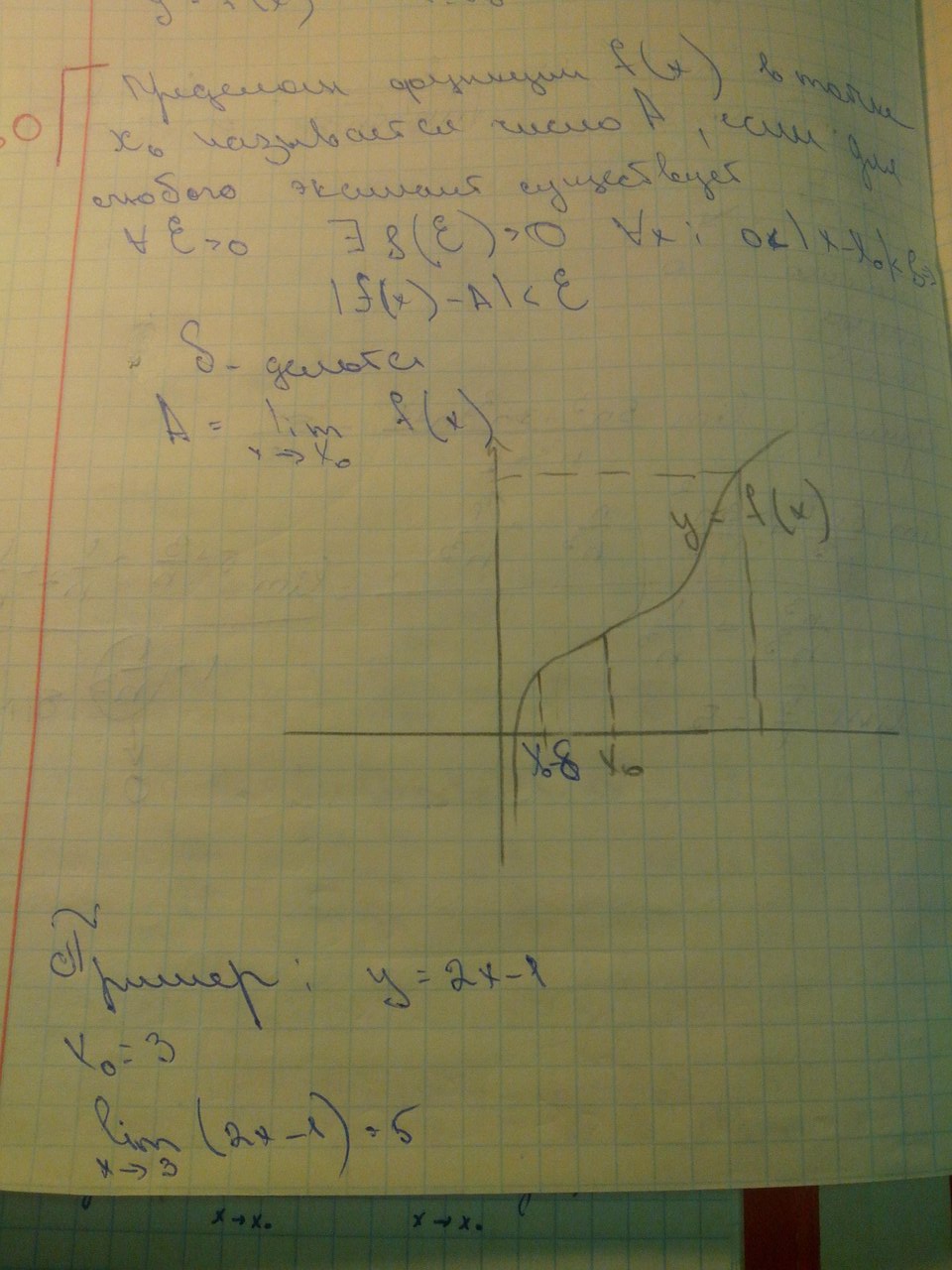
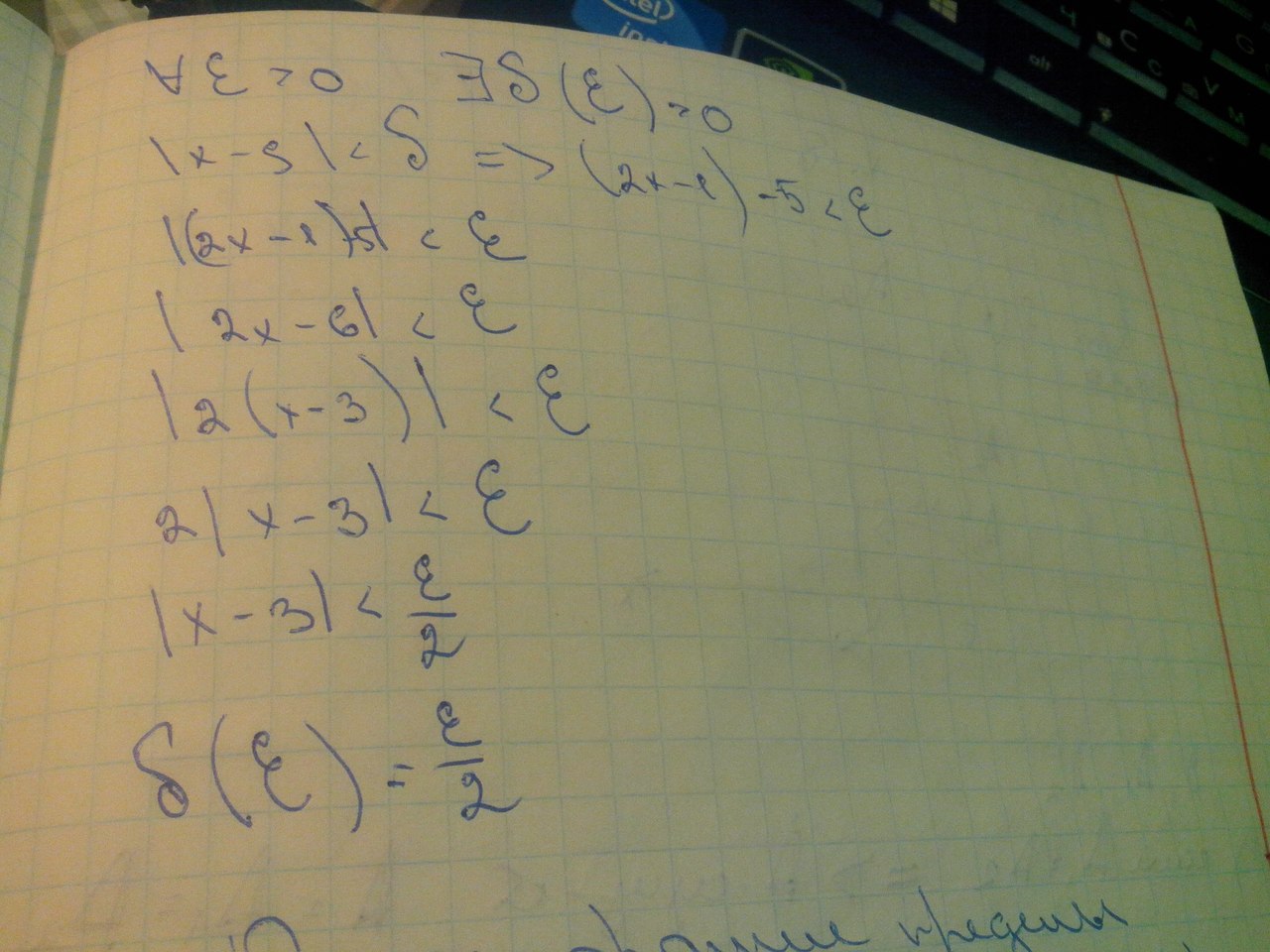
Вопрос 61:Св-ва предела функции

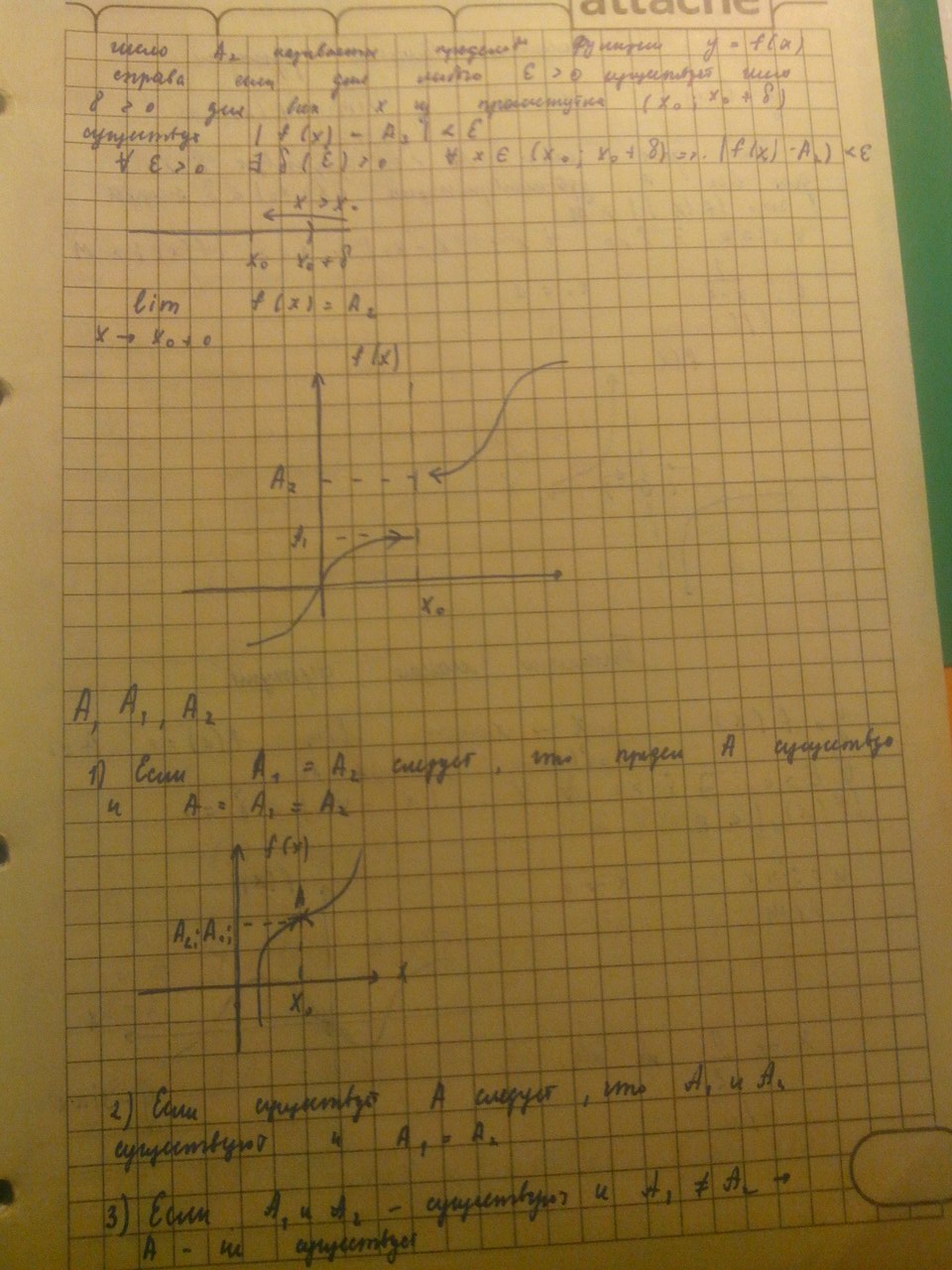
Вопрос 62:Первый замечательный предел

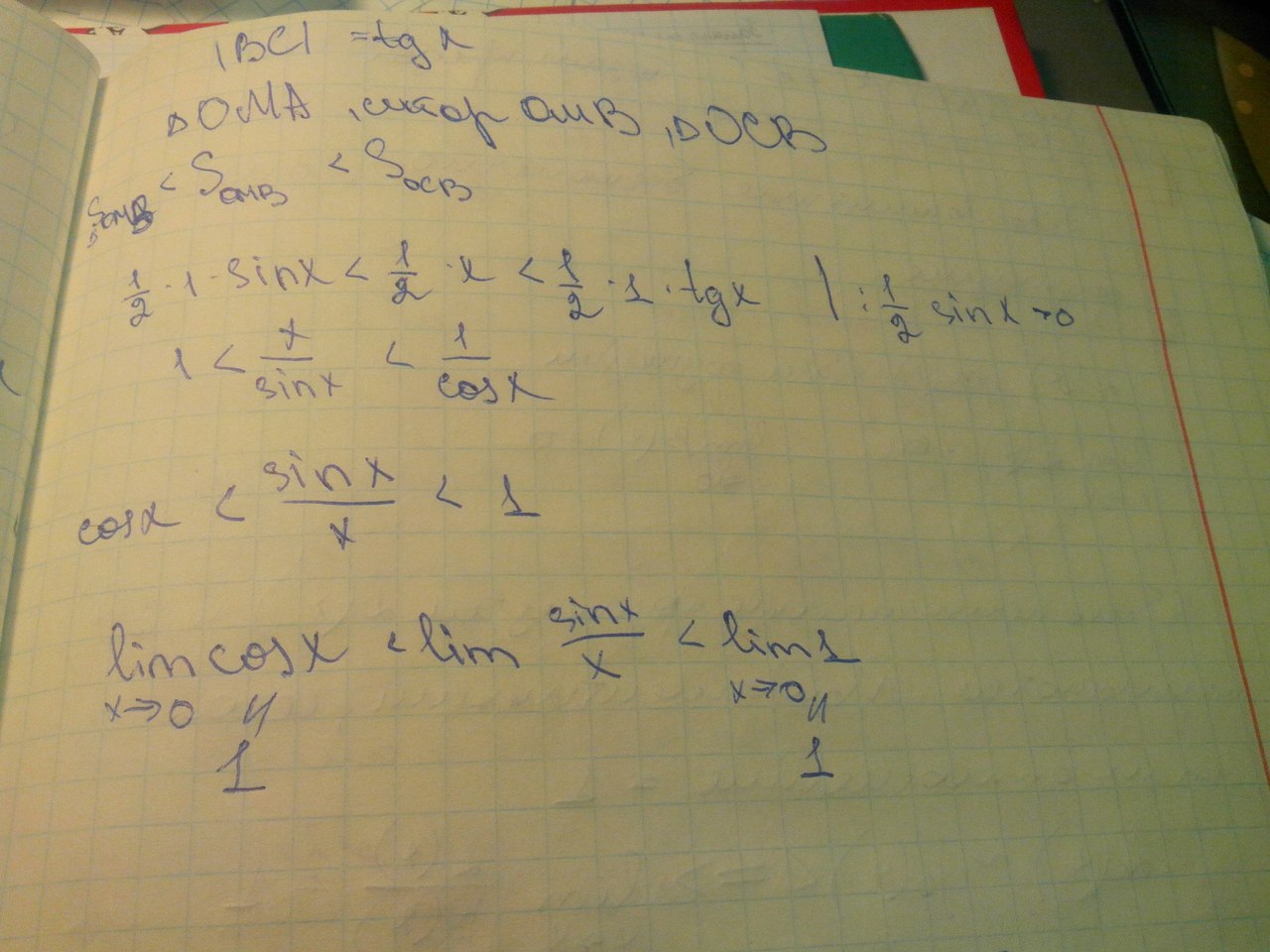
Вопрос 63:Второй замечательный предел

Вопрос 64:Непрерывность функции

Вопрос 65:Классификация точек разрыва функции

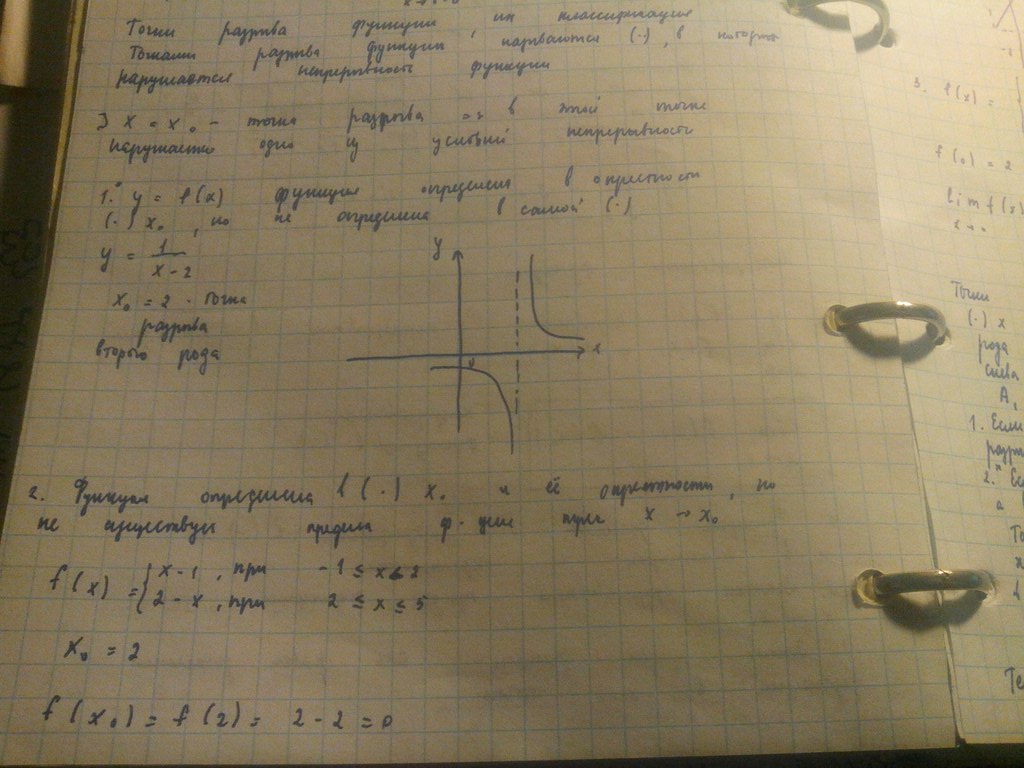
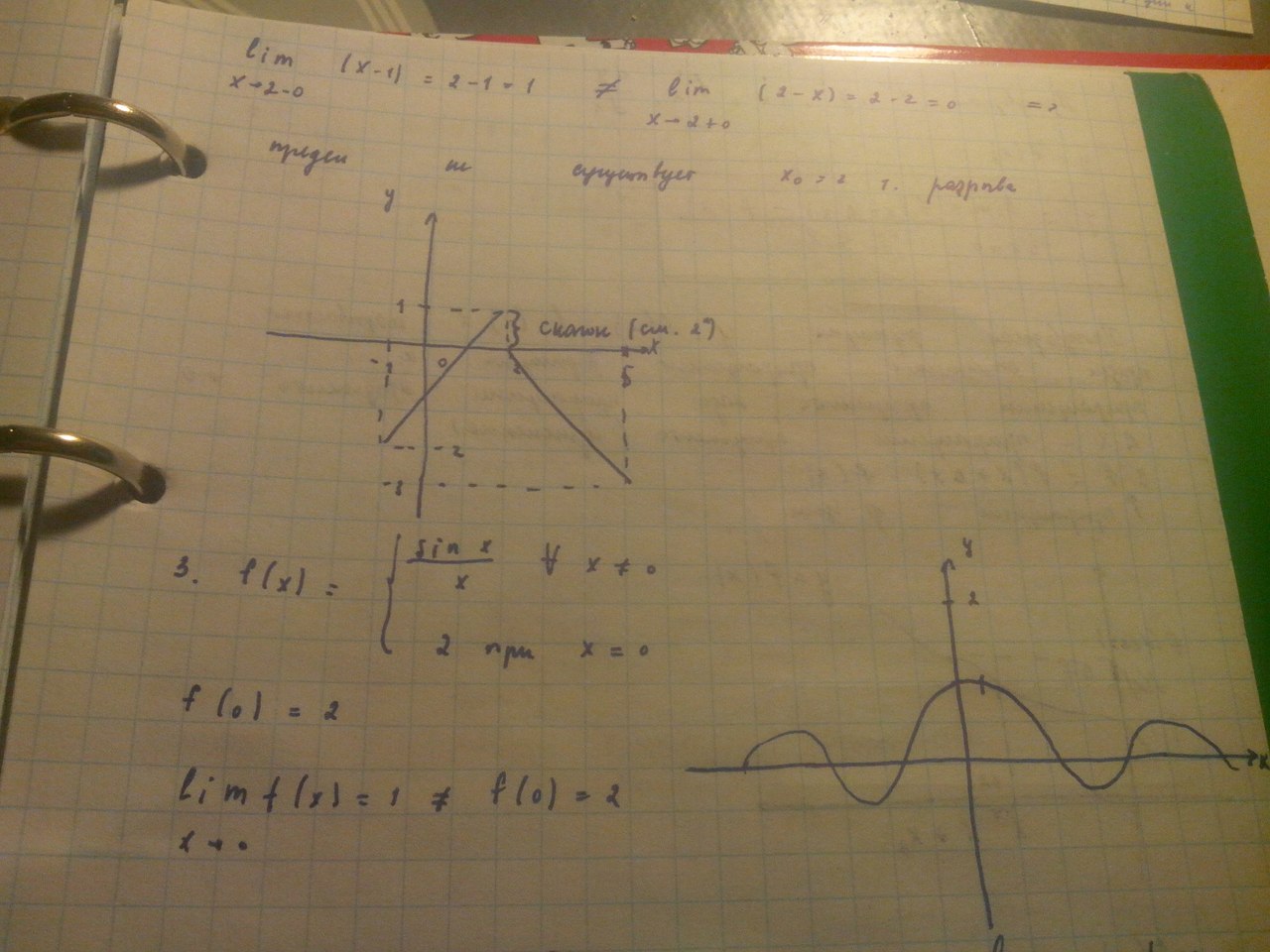
Вопрос 67:Понятие производной. Геометрический смысл производной

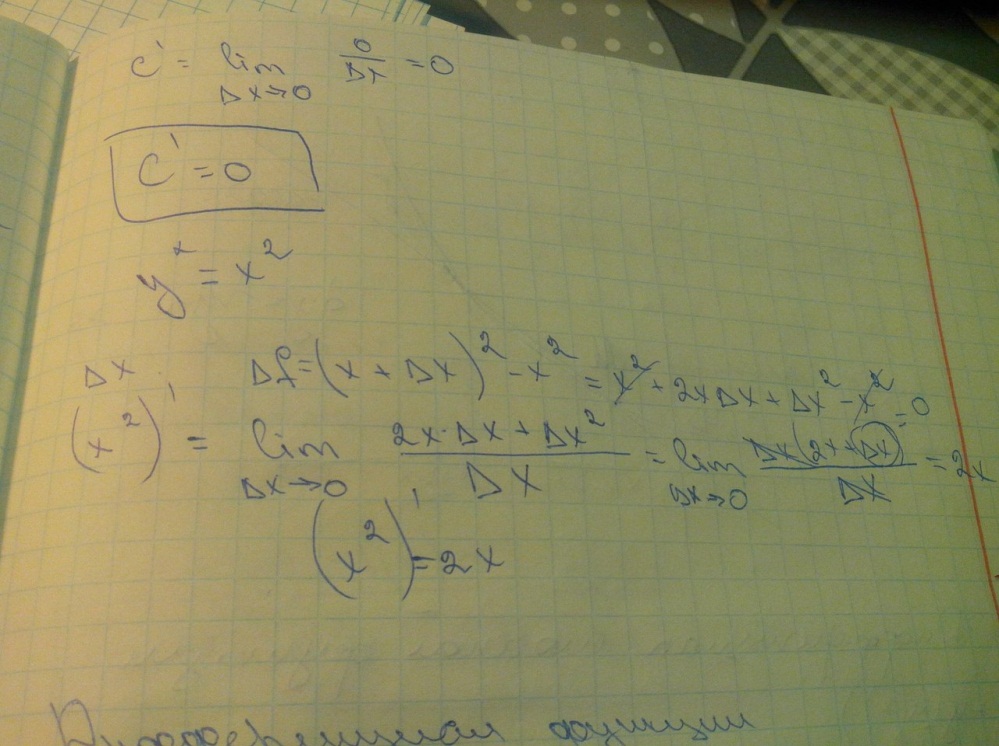
Вопрос 68:Дифференцируемость функции. Дифференциал

Вопрос 69:Правила дифференцирования

Вопрос 70:Производная обратной функции и сложной функции

Вопрос 71:Асимптоты функции

Вопрос 72:Необходимое и достаточное условие локального экстремума.Исследование на монотонность

Вопрос 73:Промежутки выпуклости.Необходимое и достаточное условие точки перегиба

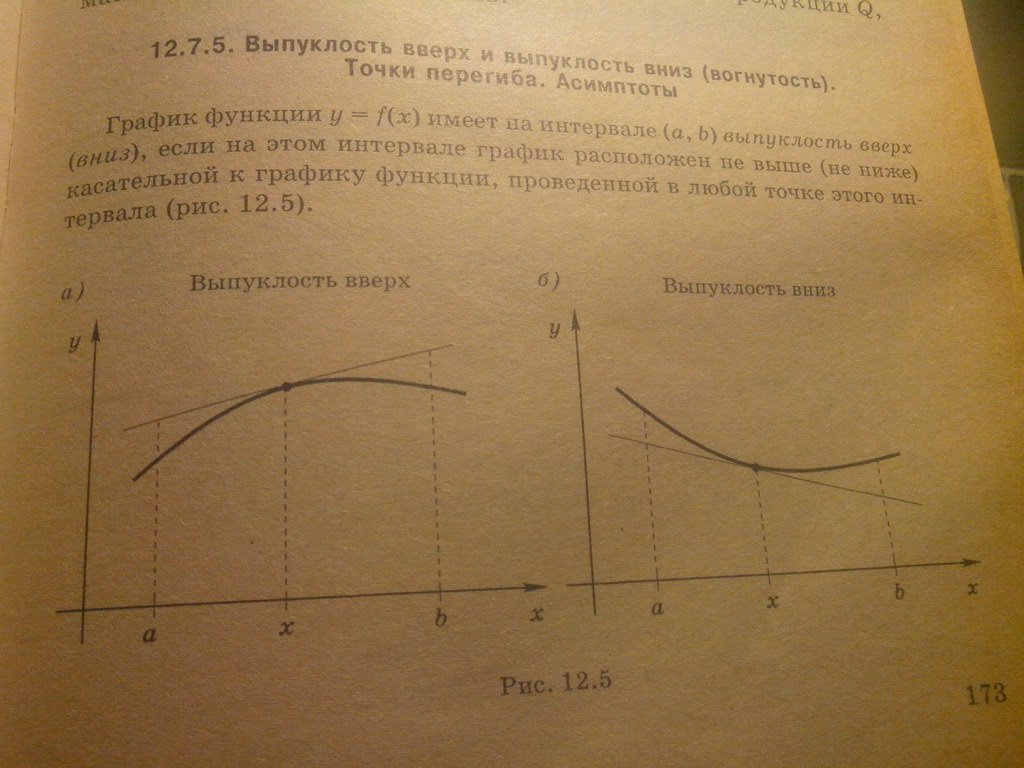
Вопрос 74:Правило Лопиталя раскрытия неопределенностей

Поиск по сайту: