Вопрос. Гипербола

. Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (ее обозначают через 2а), причем эта постоянная меньше расстояния между фокусами.

Если поместить фокусы гиперболы в точках и , то получим каноническое уравнение гиперболы

,

где . Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки и называются вершинами гиперболы. Отрезок 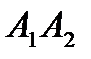такой, что 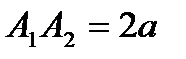, называется действительной осью гиперболы, а отрезок такой, что , - мнимой осью. При этом .

Прямая называется асимптотой гиперболы, если расстояние точки М(х;у) гиперболы этой прямой стремится к нулю при или . Гипербола имеет две асимптоты, уравнения

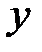
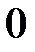
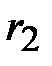
которых . На рисунке 7 указано взаимное расположение гиперболы и ее асимптот. Отношение называется эксцентриситетом гиперболы

Фокальные радиус-векторы правой ветви гиперболы: 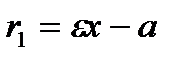(правый фокальный радиус-вектор), (левый фокальный радиус-вектор).

Фокальные радиус-векторы левой ветви гиперболы: (правый фокальный радиус-вектор), 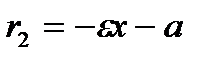(левый фокальный радиус-вектор).

По лекции:

Поиск по сайту: