Механическая энергия

Энергией называется скалярная физическая величина, являющаяся единой мерой различных видов движения материи, а также мерой перехода движения из одних форм в другие. Механическая энергия есть мера изменения энергии в различных процессах: 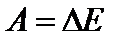. Она характеризует способность тел совершать работу. В механике различают два вида энергии: потенциальную и кинетическую.

Кинетической энергией называют энергию, зависящую от скорости движения тела.

Пусть в начальной точке пути скорость стала равной ₁, а в конечной точке пути ₂. Выражение для второго закона Ньютона умножим скалярно на : .

Получим в правой части – элементарно малая работа на малом участке dr. В левой части векторы и сонаправлены, то . Тогда: . После интегрирования получим работу А₁₂:

= . (1)

Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии этого тела. Отсюда вытекает формула, определяющая кинетическую энергию тела: , где С – произвольная постоянная. В классической механике принято С = 0. Тогда: .

Энергия тела может быть связана не только с его движением. Потенциальной называется энергия, зависящая от взаимного расположения тел или взаимодействия частей одного и того же тела.

Потенциальной энергией обладают, в частности, тела, взаимодействующие между собой посредством потенциальных (или, по-иному, консервативных) сил, то есть таких сил, работа которых не зависит от вида траектории движения тела, а определяется только положением начальной и конечной точек траектории. Работа в потенциальном поле, совершаемая по замкнутому пути, равна нулю.

Например, работа в поле силы тяжести не зависит от траектории движения тела и равна произведению модуля силы тяжести на разность высот в начальном и конечном положениях.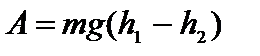

При движении вниз работа силы тяжести положительная. при движении вверх – отрицательна. Работа силы тяжести по замкнутой траектории равна нулю. Перепишем и преобразуем:

, где .

Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком.

Потенциальная энергия упруго деформированного тела: .

Таким образом, потенциальная энергия – это физическая величина, элементарное изменение которой равно (взятой со знаком минус) элементарной работе, совершаемой силами поля.

(2)

Отсюда вытекает, что физический смысл имеет лишь разность потенциальных энергий. Условимся считать, что когда тело находится на бесконечности (), то его потенциальная энергия равна нулю. Тогда под потенциальной энергией следует понимать работу, совершаемую силами поля при перемещении тела из данной точки поля в бесконечность.

Приравнивая правые части в соотношениях (1) и (2):

= ,

приходим к результату:

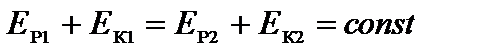(3)

Назовем полной механической энергией величину: .

Из (3) вытекает, что полная механическая энергия тела при его перемещении вдоль любой траектории в потенциальном поле остается постоянной.

Можно показать также, что изменение полной механической энергии в незамкнутой консервативной системе равно работе внешних сил.

Если консервативная система замкнута, то внешние силы отсутствуют: Þ Þ E = const.

закон сохранения энергии замкнутой консервативной системы:

Полная механическая энергия замкнутой системы тел, взаимодействующих между собой посредством потенциальных сил, остается неизменной при любом движении этих тел.

Если система подвергается действию неконсервативных (диссипативных) сил, механическая энергия убывает, переходя в другие виды энергии (например, тепловую при действии сил трения). Но в целом энергия остается постоянной.

Согласно всеобщему закону сохранения и превращения энергии уменьшение или увеличение полной механической энергии системы в точности компенсируется увеличением или уменьшением какого-либо другого вида энергии. Энергия никуда не исчезает и не появляется вновь, а лишь переходит от одного тела к другому или превращается из одного вида в другой.

Поиск по сайту: