 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Момент импульса. Закон сохранения момента импульса. Введем определение еще одной величины, характеризующей вращение твердого тела – момента импульса или момента количества движения тела относительно оси
Введем определение еще одной величины, характеризующей вращение твердого тела – момента импульса или момента количества движения тела относительно оси вращения.
Для i -й материальной точки, имеющей линейную скорость  Момент импульса или момент количества движения относительно оси вращения определяется как:
Момент импульса или момент количества движения относительно оси вращения определяется как:  .
.
[ L ]=кг.м2/с.
Этот вектор является также направленным вдоль оси вращения и также в сторону, определяемую правилом буравчика. Так как  , то модуль вектора
, то модуль вектора 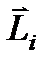 равен
равен  . Величина полного момента импульса твердого тела равна арифметической сумме моментов импульса всех его точек, так как при вращении тела все его точки вращаются в одном и том же направлении:
. Величина полного момента импульса твердого тела равна арифметической сумме моментов импульса всех его точек, так как при вращении тела все его точки вращаются в одном и том же направлении:  .
.
Момент импульса определяется формулой  и является вектором, совпадающим по направлению с вектором угловой скорости.
и является вектором, совпадающим по направлению с вектором угловой скорости.
Будем считать, что момент инерции I остается все время постоянным, а угловая скорость изменяется со временем, так что  . Продифференцируем
. Продифференцируем  по времени:
по времени: 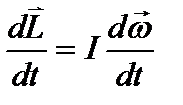 , Þ
, Þ 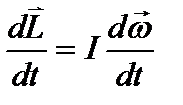 Þ
Þ 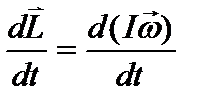 .
.
Сопоставляя полученное выражение с основным законом динамики вращательного движения, можно его записать в виде:  .
.
В замкнутой системе момент внешних сил  и Þ
и Þ  , откуда:
, откуда:  ,
,
где  – векторная сумма моментов тел, входящих в эту систему.
– векторная сумма моментов тел, входящих в эту систему.
Данное выражение представляет собой закон сохранения момента импульса: сумма моментов импульса всех тел замкнутой системы сохраняется, то есть не изменяется с течением времени:
 .
.
Закон сохранения момента импульса проявляется как в технике (например, в устройстве вертолета – для изменения ориентации), так и в природе (вращение Земли вокруг своей оси происходит с постоянной угловой скоростью, поскольку не изменяется ее момент инерции).
Поиск по сайту: