 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Замедление времени, сокращение длины
Исходя из постулатов, рассмотренных выше, должны быть получены такие преобразования, чтобы значение скорости света не зависело от движения источника или приемника света. Такая форма преобразования координат и времени получила название преобразований Лоренца.
Пусть имеется некоторая система координат К  , в которой источник неподвижен, и пусть также имеется некоторая движущаяся система координат К’, в которой наблюдатель измеряет параметры
, в которой источник неподвижен, и пусть также имеется некоторая движущаяся система координат К’, в которой наблюдатель измеряет параметры 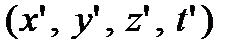 (рси. 23.1). Предположим, что начало отсчета времени t’ совпадает с началом отсчета t и что в этот нулевой момент времени начала координат систем К и К’ также совпадают. Предположим, система к’ движется в сторону (+ х) со скоростью v относительно системы К. Тогда преобразования Лоренца будут выглядеть следующим образом:
(рси. 23.1). Предположим, что начало отсчета времени t’ совпадает с началом отсчета t и что в этот нулевой момент времени начала координат систем К и К’ также совпадают. Предположим, система к’ движется в сторону (+ х) со скоростью v относительно системы К. Тогда преобразования Лоренца будут выглядеть следующим образом:


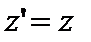
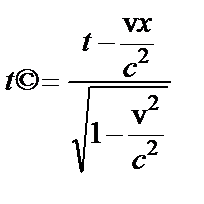 (1).
(1).
Из преобразований Лоренца следует, что время относительно, то есть меняется при переходе от одной системы отсчета к другой.
Если изменить направление скорости на противоположное, то вместо (1) можно получить обратное преобразование:
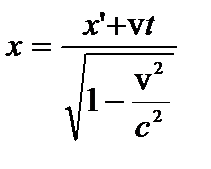

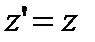
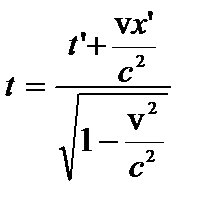 (2).
(2).
Одинаковый вид (1) и (2) является следствием полного равноправия систем отсчета (относительности движения), то есть любая из систем К и К’ может быть принята за неподвижную, при этом будет изменяться только знак относительной скорости.
При малых скоростях, когда можно считать 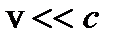 , преобразования Лоренца переходят в преобразования Галилея. Это свидетельствует о том, что теория относительности не отвергает классическую механику, но рассматривает ее как частный случай малых относительных скоростей. Таким образом, СТО указывает на границы применимости классической механики.
, преобразования Лоренца переходят в преобразования Галилея. Это свидетельствует о том, что теория относительности не отвергает классическую механику, но рассматривает ее как частный случай малых относительных скоростей. Таким образом, СТО указывает на границы применимости классической механики.
СТО называется релятивистской теорией, а явления, описываемы этой теорией – релятивистскими. Механика, описывающая движения с релятивистскими (близкими к с) скоростями, называется релятивистской механикой.
Относительность одновременности событий. Одновременными будем считать два события, происходящие в разных точках  некоторой системы отсчета, если они происходят в один и тот же момент по часам этой системы отсчета.
некоторой системы отсчета, если они происходят в один и тот же момент по часам этой системы отсчета.
Рассмотрим вновь две системы отсчета: неподвижной К и движущейся К’. Пусть в каждой из систем находится неподвижный относительно собственной системы наблюдатель. Предположим, что в системе К в точках с координатами  происходят одновременно два события в момент времени
происходят одновременно два события в момент времени  . Для наблюдателя в системе К одновременность событий означает, что
. Для наблюдателя в системе К одновременность событий означает, что  . Для наблюдателя в системе К’ этим событиям, как следует из преобразований Лоренца, будут соответствовать координаты:
. Для наблюдателя в системе К’ этим событиям, как следует из преобразований Лоренца, будут соответствовать координаты:  ;
; 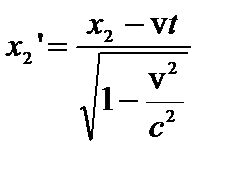
и моменты времени:  ;
; 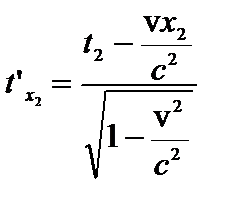 .
.
Для проверки одновременности событий наблюдатель в К’ системе должен из  вычесть
вычесть 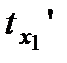 :
:  ,
,
то есть события в неподвижной системе для наблюдателя в движущейся системе К’ происходят не одновременно. Из полученной формулы следует, что в системе К’ события будут одновременными только при 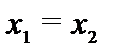 , то есть события в одной точке.
, то есть события в одной точке.
Таким образом понятие одновременности не абсолютно.
Замедление времени. Пусть в движущейся системе отсчета К’ в неподвижной точке х ’ произошло событие длительностью 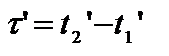 , где
, где  моменты начала и конца события по часам, покоящимся в системе К’. Наблюдатель в неподвижной системе К отметит по часам своей системы начало и конец события в моменты
моменты начала и конца события по часам, покоящимся в системе К’. Наблюдатель в неподвижной системе К отметит по часам своей системы начало и конец события в моменты 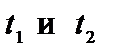 , которые будут связаны с моментами
, которые будут связаны с моментами  преобразованиями Лоренца (при учете того, что х неизменно):
преобразованиями Лоренца (при учете того, что х неизменно):  ;
;  . Тогда:
. Тогда:
 (1)
(1)
 Итак, продолжительность события в системе К
Итак, продолжительность события в системе К 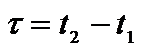 и К’
и К’  не совпадают. Интервал, измеренный часами, неподвижными в данной системе отсчета, называются собственным интервалом. Интервал для движущейся системы К’ оказывается больше, чем для неподвижной К, то есть процессы в движущейся системе длятся дольше, чем в неподвижной.
не совпадают. Интервал, измеренный часами, неподвижными в данной системе отсчета, называются собственным интервалом. Интервал для движущейся системы К’ оказывается больше, чем для неподвижной К, то есть процессы в движущейся системе длятся дольше, чем в неподвижной.
Таким образом, ход времени для движущейся системы отсчета замедляется относительно неподвижной системы.
Сокращение длины. Пусть в системах К и К’ рассматривается объект, который неподвижен относительно системы К’ и двигается с ней со скоростью v вдоль оси х. Допустим, что размеры объекта определяются координатами в К’ системе  . Тогда собственные размеры (в К’ системе) объекта можно представить в виде:
. Тогда собственные размеры (в К’ системе) объекта можно представить в виде:  , причем координаты
, причем координаты  определятся для одного момента времени t’.
определятся для одного момента времени t’.
Для наблюдателя, покоящегося в неподвижной К системе размеры объекта будут определяться выражениями:  .
.
Из преобразований Лоренца определим связь между 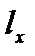 и
и  :
:
 ;
; 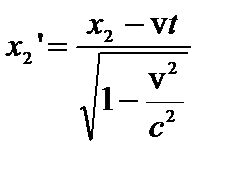 Þ
Þ  Þ
Þ
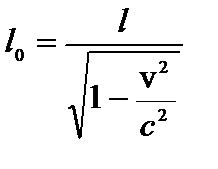 или
или 
Из полученного выражения следует, что длина стержня зависит от скорости его движения относительно системы отсчета. Если  , то подкоренное выражение стремится к единице и
, то подкоренное выражение стремится к единице и 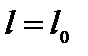 , то есть при малых скоростях длина стержня во всех инерциальных системах отсчета одинакова. Если
, то есть при малых скоростях длина стержня во всех инерциальных системах отсчета одинакова. Если  , то чем больше скорость движение стержня, тем меньше его длина, измеренная в этой системе. Из формулы для Лоренцева сокращения длины следует, что тела не могут двигаться со скоростями
, то чем больше скорость движение стержня, тем меньше его длина, измеренная в этой системе. Из формулы для Лоренцева сокращения длины следует, что тела не могут двигаться со скоростями 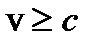 , так как при
, так как при  длина
длина 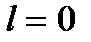 , а при
, а при 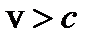
 должна быть мнимой.
должна быть мнимой.
Поиск по сайту: