Модели в механике. Система отсчета. Материальная точка. Траектория, длина пути, вектор перемещения

Механическое движение – изменение положения тела относительно других тел с течением времени.

Материальная точка – это модель тела, размерами и формой которого можно пренебречь по сравнению с масштабами движения.

Любое движение твердого тела можно представить как комбинацию поступательного и вращательного движения. Поступательное движение – это движение, при котором любая прямая жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения.

Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение.

Тела отсчета – тела, относительно которых определяется или изучается положение данного движущегося тела. Система отсчета – это тело отсчета, связанная с ним система координат и способ измерения времени (часы). Траектория – линия, которую описывает материальная точка в пространстве при движении. В зависимости от формы траектории движение может прямолинейным и криволинейным. Расстояние, пройденное телом, с момента начала отсчета времени, называется длиной пути. Это длина траектории. Обозначения: L, S, DS. Вектор, соединяющий начальное положение с последующим положением, называют перемещением. Обозначения: 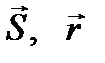, D . Вектор, соединяющий некоторую фиксированную точку пространства с данной движущейся точкой, называется радиус-вектором.

Þ ,

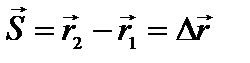перемещение равно изменению радиуса-вектора. Если точку 0 совместить с точкой 1, то 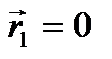, Þ

перемещение равно радиусу-вектору.

В декартовой системе координат, используемой наиболее часто, положение точки в данный момент времени по отношению к этой системе характеризуется тремя координатами x, y, z или радиусом-вектором. При этом проекции радиуса-вектора на оси системы отсчета эквивалентны координатам материальной точки x, y, z:

При движении материальной точки ее координаты с течением времени изменяются. Уравнение движения материальной точки может быть задано 3-мя способами: а) координатный , б) векторный: (эквивалентен координатному); в) траекторный (естественный) .)

2. Кинематика материальной точки. Скорость и ускорение.

Кинематика – это раздел механики, изучающий движение тел без учета взаимодействия, то есть без учета причин, вызывающих это движение.

Введем понятие скорости материальной точки. Пусть за промежуток времени Dt материальная точка переместилась из точки 1 в точку 2 (см. рис. 1.2). Средняя скорость определяет путь, пройденный в единицу времени. Вектор перемещения материальной точки представляет собой приращение радиуса-вектора за промежуток времени D t = t ₂- t ₁: 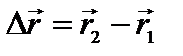. Вектор средней скорости совпадает по направлению с вектором . Определим вектор мгновенной скорости (или вектор скорости) материальной точки как предел отношения /Dt при Dtà0, то есть . Это значит, что вектор скорости материальной точки в данный момент времени равен производной от радиуса-вектора по времени и направлен по касательной к траектории в данной точке в сторону движения материальной точки. Модуль вектора .

Другим понятием, характеризующим движение точки, является ускорение. Ускорение – это физическая величина, характеризующая быстроту изменения скорости.

Среднее ускорение – это отношения изменения скорости ко времени, за которое это изменение произошло. Вектор среднего ускорения: , где – вектор изменения скорости за промежуток времени Dt. Переходя к пределу, получим вектор мгновенного ускорения: 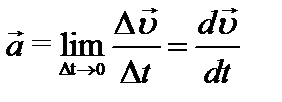, т.е. вектор ускорения материальной точки равен производной от скорости по времени. Направление вектора ускорения совпадает с направлением вектора 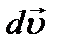(приращением вектора за время dt).

При использовании для описания движения прямоугольной декартовой системы координат положение материальной точки задается тремя координатами x, y, z. При движении точки эти координаты изменяются во времени и, следовательно ее движение описывается тремя уравнениями x (t), y (t), z (t). В этом случае вектор скорости может быть разложен на три взаимно перпендикулярные компоненты: 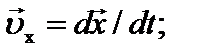, причем , а вектор ускорения – на компоненты: , причем .

Поиск по сайту: