Реальные газы. Уравнение Ван-дер-Ваальса. Критическое состояние

Реальным называется газ, между молекулами которого действуют силы межмолекулярного взаимодействия, состоящие из сил притяжения и сил отталкивания.

Для получения уравнения состояния реального газа необходимо учесть собственный объем молекул и энергию взаимодействия молекул на расстоянии. Наличие собственного объема молекул приводит к уменьшению объема, предоставленного молекулам, на некоторую величину. Силы притяжения между молекулами газа вызывают уменьшение давления молекул газа на стенки сосуда на некоторую величину р_i.

Это уравнение может получено путем соответствующего изменения уравнения Менделеева-Клапейрона путем внесения в него поправок.

Уравнение состояния реального газа (уравнение Ван-дер-Ваальса) для одного моля имеет вид:

,

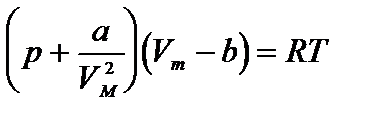где р - давление, оказываемое на стенки сосуда, V_М – объем одного моля газа, а и b - постоянные Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые опытным путем. Поправка – внутреннее давление, обусловленное силами взаимного притяжения между молекулами. Поправка b характеризует ту часть объем, которая недоступна для движения молекул. Она равна учетверенному собственному объему молекул, содержащихся в моле газа:

b = N_A.

Уравнение Ван-дер-Ваальса для произвольной массы газа имеет вид:

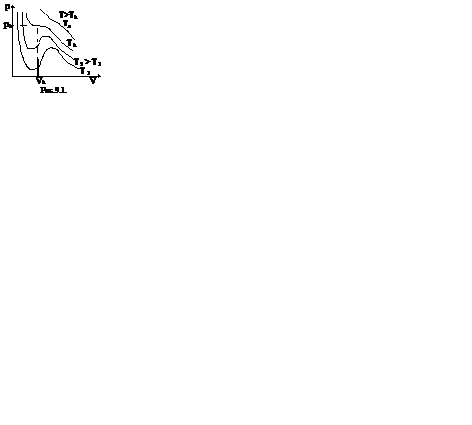
Уравнение Ван-дер-Ваальса позволяет построить теоретические изотермы реального газа и сравнить их с изотермами идеального газа и экспериментальными изотермами реального газа.

Уравнение Ван-дер-Ваальса после нескольких преобразований можно записать в виде:

.

Это уравнение третьей степени относительно V. Кубическое уравнение может иметь либо три вещественных корня, либо один вещественный и два мнимых.

Первому случаю соответствуют изотермы при низких температурах – кривые для Т₁ и Т₂ (рис.9.1.) Второму случаю изотермы при высоких температурах (одно значение объема V отвечает одному значению давления р), то есть любая изотерма начиная от изотермы для Т_к.

Совпадение изотерм идеального и реального газа наблюдается при малых давлениях и больших объемах (так как при этих условиях газ можно считать идеальным). Для семейства изотерм Ван-дер-Ваальса характерно так называемой критической изотермы (при температуре Т_к) имеющий точку перегиба при некотором давлении р_к и объеме V_к; при Т>Т_к все изотермы идут монотонно, при Т < Т_к все изотермы имеют минимум и максимум.

Экспериментальные изотермы, снятые при температурах выше критической, отражают монотонное увеличение давлений газа при уменьшении его объема. При температурах, меньше критической, эксперимент показывает, что изотермы на участке 2,6 имеют «полочку». Часть 6–7 отвечает газообразному состоянию, а часть 1–2 – жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6-2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.

Состояния на участке 3–4–5 не наблюдаются экспериментально; состояния 2–3 и 5–6 могут быть реализованы при особых условиях. Участок 2–3 соответствует т.н. перегретой жидкости. Участок 5-6 – пересыщенному пару (рис.9.2). Эти неустойчивые состояния называются метастабильными. Горизонтальный участок реальной изотермы расположен так, что площади, ограниченные им и теоретической изотерме. В обоих случаях работа должна быть одинакова, следовательно, указанные выше площади должны быть равновелики.

Уравнение Ван-дер-Ваальса описывает не только свойства газов и паров, но и жидкостей. Анализ изотерм реального газа показывает, что превращение реального газа в жидкость возможно только при температурах, меньших критической, и при соответствующих давлениях.

Поиск по сайту: