Колебательное движение. Гармонические колебания

Движения, обладающие той или иной степенью повторяемости, называются колебаниями.

Если значения физических величин, изменяющихся в процессе движения, повторяются через равные промежутки времени, то такое движение называется периодическим. В зависимости от физической природы колебательного процесса различают механические и электромагнитные колебания. По способу возбуждения колебания делят на: свободные (собственные), происходящие в представленной самой себе системе около положения равновесия после какого-либо первоначального воздействия; вынужденные – происходящие при периодическом внешнем воздействии.

Условия возникновения свободных колебаний: а) при выведении тела из положения равновесия в системе должна возникнуть сила, стремящаяся вернуть его в положение равновесия; б) силы трения в системе должны быть достаточно малы.

А мплитуда А – модуль максимального отклонения колеблющейся точки от положения равновесия.

Колебания точки, происходящие с постоянной амплитудой, называют незатухающими, а колебания с постепенно уменьшающейся амплитудой – затухающими.

Время, в течение которого совершается полное колебание, называют периодом (Т).

Частотой 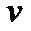периодических колебаний называют число полных колебаний, совершаемых за единицу времени:

Единица частоты колебаний — герц (Гц). Герц – это частота колебаний, период которых равен 1 с: 1 Гц = 1 с ^–1.

Циклической или круговой частотой периодических колебаний называется число полных колебаний, совершаемых за время 2p с: . [ ]=рад/с.

Гармонические – это такие колебания, которые описываются периодическим законом:

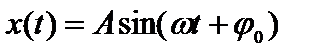или (1)

где 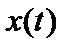– периодически изменяющаяся величина (смещение, скорость, сила и т.д.), А – амплитуда.

Система, закон движения которой имеет вид (1), называется гармоническим осциллятором. Аргумент синуса или косинуса 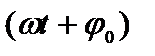называется фазой колебаний. Фаза колебания определяет смещение в момент времени t. Начальная фаза 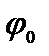определяет смещение тела в момент начала отсчета времени.

Рассмотрим смещение x колеблющегося тела относительно положения равновесия. Уравнение гармонического колебания:

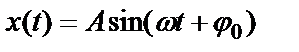
Первая производная от по времени дает выражение для скорости движения тела: ; (2)

Скорость достигает своего максимального значения в момент времени, когда 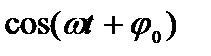=1: . Смещение же точки в этот момент рано нулю 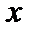=0 (рис. 17.1, б).

Ускорение изменяется со временем также по гармоническому закону:

, (3)

где 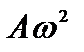– максимальное значение ускорения. Знак минус означает, что ускорение направлено в сторону, противоположную смещению, т.е. ускорение и смещение изменяются в противофазе (рис. 17.1 в). Видно, что скорость достигает максимального значения, когда колеблющаяся точка проходит положение равновесия. В этот момент смещение и ускорение равны нулю.

Для того чтобы тело совершало гармоническое колебательное движение, на него должна действовать сила, всегда направленная к положению равновесия, а по величине – прямо пропорциональная смещению от этого положения. Силы, направленные к положению равновесия, называются возвращающими.