Вынужденные колебания. Переменный ток

Процессы, возникающие в электрических цепях под действием внешнего периодического источника тока, называются вынужденными колебаниями.

Вынужденные колебания, в отличие от собственных колебаний в электрических цепях, являются незатухающими. Периодический внешний источник обеспечивает приток энергии к системе и не дает колебаниям затухать, несмотря на наличие неизбежных потерь.

Особый интерес представляет случай, когда внешний источник, напряжение которого изменяется по гармоническому закону с частотой ω, включен в электрическую цепь, способную совершать собственные свободные колебания на некоторой частоте ω₀.

Если частота ω₀ свободных колебаний определяется параметрами электрической цепи, то установившиеся вынужденные колебания всегда происходят на частоте ω внешнего источника.

Для установления стационарных вынужденных колебаний необходимо некоторое время Δt после включения в цепь внешнего источника. Это время по порядку величины равно времени τ затухания свободных колебаний в цепи.

Электрические цепи, в которых происходят установившиеся вынужденные колебания под действием периодического источника тока, называются цепями переменного тока.

Рассмотрим последовательный колебательный контур, то есть RLC-цепь, в которую включен источник тока, напряжение которого изменяется по периодическому закону (рис. 2.3.1): e(t) = 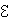₀ cos ωt,

где 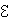₀ – амплитуда, ω – круговая частота.

Рисунок 2.3.1. Вынужденные колебания в контуре.

Предполагается, что для электрической цепи, изображенной на рис. 2.3.1, выполнено условие квазистационарности. Поэтому закон Ома можно записать для мгновенных значений токов и напряжений:

Величина – это перенесенная с изменением знака из правой части уравнения в левую ЭДС самоиндукции катушки. Эту величину принято называть напряжением на катушке индуктивности.

Уравнение вынужденных колебаний можно записать в виде

u_R + u_C + u_L = e(t) = 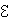₀ cos ωt,

где u_R(t), u_C(t) и u_L(t) – мгновенные значения напряжений на резисторе, конденсаторе и катушке соответственно. Амплитуды этих напряжений будем обозначать буквами U_R, U_C и U_L. При установившихся вынужденных колебаниях все напряжения изменяются с частотой ω внешнего источника переменного тока. Для наглядного решения уравнения вынужденных колебаний можно использовать метод векторных диаграмм.

На векторной диаграмме колебания определенной заданной частоты ω изображаются с помощью векторов.

Изображение гармонических колебаний A cos (ωt + φ1), B cos (ωt + φ2) и их суммы C cos (ωt + φ) с помощью векторов на векторной диаграмме.

Длины векторов на диаграмме равны амплитудам колебаний A и B, а наклон к горизонтальной оси определяется фазами колебаний φ₁ и φ₂. Взаимная ориентация векторов определяется относительным фазовым сдвигом Δφ = φ₁ – φ₂. Вектор, изображающий суммарное колебание, строится на векторной диаграмме по правилу сложения векторов:

Для того чтобы построить векторную диаграмму напряжений и токов при вынужденных колебаниях в электрической цепи, нужно знать соотношения между амплитудами токов и напряжений и фазовый сдвиг между ними для всех участков цепи.

Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R, конденсатору емкости C и катушки индуктивности L. Во всех трех случаях напряжения на резисторе, конденсаторе и катушке равны напряжению источника переменного тока.

1. Резистор в цепи переменного тока

Здесь через I_R обозначена амплитуда тока, протекающего через резистор. Связь между амплитудами тока и напряжения на резисторе выражается соотношением RI_R = U_R.

Фазовый сдвиг между током и напряжением на резисторе равен нулю.

2. Конденсатор в цепи переменного тока

Соотношение между амплитудами тока I_C и напряжения U_C:

Ток опережает по фазе напряжение на угол

2. Катушка в цепи переменного тока

Соотношение между амплитудами тока I_L и напряжения U_L:

ωLI_L = U_L.

Ток отстает по фазе от напряжения на угол

Теперь можно построить векторную диаграмму для последовательного RLC-контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I₀. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги. Векторная диаграмма для последовательного RLC-контура изображена на рис. построена для случая, когда 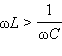или 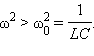В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.

Из рисунка видно, что

откуда следует

Величину

называют полным сопротивлением цепи переменного тока. Формулу, выражающую связь между амплитудными значениями тока и напряжения в цепи, можно записать в виде

Z I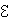₀ = ₀.

Это соотношение называют законом Ома для цепи переменного тока. Из выражения для I₀ видно, что амплитуда тока принимает максимальное значение при условии

или

Явление возрастания амплитуды колебаний тока при совпадении частоты ω внешнего источника с собственной частотой ω₀ электрической цепи называется электрическим резонансом. При резонансе

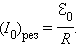
Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов R, L и C (так называемый резонанс токов).

При последовательном резонансе (ω = ω₀) амплитуды U_C и U_L напряжений на конденсаторе и катушке резко возрастают:

В § 2.2 было введено понятие добротности RLC-контура:

Таким образом, при резонансе амплитуды напряжений на конденсаторе и катушке в Q раз превышают амплитуду напряжения внешнего источника.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

а) основная литература:

1. Волькенштейн В.С. Сборник задач по физике. - М.: Наука, 1985.

2. Калашников С.Г. Электричество. –М.: Наука, 1983.

3. Ремизов А.Н., Потапенко А.Я. Курс физики. – М.: Дрофа, 2002.

4. Савельев И.В. Курс общей физики в 5 кн.: кн.2: электричество и магнетизм. – М.: АСТ: Астрель, 2005.

5. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2000.

6. Чертов А.Г., Воробьев А.А. Задачник по физике. - М.: Изд-во Физико-математической литературы, 2006.

б) дополнительная литература:

1. Гельфгат И.М., Генденштейн Л. Э., Кирик Л. А. 1001 задача по физике. – М.: «Илекса», 2001.

2. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1989.

3. Дмитриева В.Ф., Прокофьев В.Л. Основы физики. – М.: Высшая школа, 2001.

4. Зисман Г.А., Тодес О.М. Курс общей физики. Т.1.–М.: Наука, 1974.

5. Кибец И.Н., Кибец В.И. Физика: Справочник. – Харьков: Фолио; Ростов-на-Дону:Феникс, 1997.

6. Макаренко Г.М. Физика. Т.1.–Мн.: ДизайнПРО, 1997.

7. Савельев И.В. Курс общей физики. Т.2.–М.: Наука, 1989.

8. Сахаров Д.И. Сборник задач по физике для вузов. – М.: ООО «Издательский дом «ОНИКС 21 век: ООО «Издательство «Мир и образование».

9. Сивухин Д.В. Общий курс физики, т.3. М.: Наука, 1977.

10. Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики. –М.: Высшая школа, 1999.

11. Физическая энциклопедия. В 5-ти т.– М.: Советская энциклопедия, Большая Российская энциклопедия, 1988–1998.

12. Цедрик М.С.(ред.) Сборник задач по курсу общей физики.- М.: Просвещение, 1989.

13. Яворский Б.М., Детлаф А.А. Физика. – М.: Дрофа, 1999.

Поиск по сайту: