Применение теоремы Гаусса

Пусть дана бесконечно большая, равномерно заряженная плоскость с поверхностной плотностью σ (поверхностная плотность заряда ). Вследствие симметрии силовые линии перпендикулярны плоскости и направлены от нее в обе стороны. Выделим элементарную площадку площадью dS (имеющих заряд dq=s·dS). В качестве замкнутой поверхности выберем цилиндр, перпендикулярный заряженной плоскости с основанием dS (рис.10). Так как образующие цилиндра параллельны линиям напряженности (cos a=0), то поток вектора смещения сквозь боковые стороны цилиндра, равен нулю. Полный поток сквозь цилиндр равна сумме потоков через его основания: .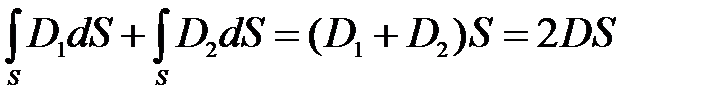

По теореме Гаусса . Откуда , или

Используя теорему Гаусса, можно определить смещение и напряженность электрического поля, создаваемого:

1) бесконечно длинной равномерно заряженной нитью или цилиндром с линейной плотностью ; или ,

где r – расстояние от нити до точки, в которой определяется смещение (напряженность);

2) равномерно заряженной сферической поверхности с общим зарядом Q:

Поиск по сайту: