Поток вектора электрического смещения. Теорема Гаусса

Напряженность электростатического поля зависит от свойств среды (ε). Кроме того, вектор напряженности 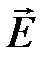, переходя через границу диэлектриков, претерпевает скачкообразное изменение, поэтому для описания (непрерывного) электрического поля системы зарядов с учетом поляризационных свойств диэлектриков вводится вектор электрического смещения (электрической индукции), который для изотропной среды записывается как

Изотропи́я, изотро́пность (из др.-греч. «равный, одинаковый, подобный» + «оборот, поворот; характер») — одинаковость физических свойств во всех направлениях, инвариантность, симметрия по отношению к выбору направления (в противоположность анизотропии).

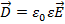
Единица электрического смещения - Кл/м².

для вакуума: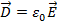

это силовая характеристика поля в вакууме.

Если есть однородное поле со смещением D, то потоком электрического смещения называется величина:

Ф=DScosα

где a – угол между нормалью к площадке S и направлением D (рис.7).

Если поле неоднородно (рис.8), то можно выбрать малую площадку dS, в рамках которой поле можно считать однородным. Поток через нее:

dФ=DdScosα

Рассчитать поток электрического смещения через любую поверхность можно по формуле: ,

где – проекция вектора D на нормаль к площадке dS: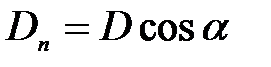

Поток вектора напряженности электрического поля определяется как: .

Теорема Гаусса позволяет определить поток вектора смещения (или напряженности) электростатического поля, создаваемого системой зарядов. Определим поток электрического смещения сквозь сферическую поверхность радиусом r, в центре которой расположен точечный заряд +q. По формуле для потока имеем .

Для точечного заряда .

Линии электрического смещения перпендикулярны поверхности сферы, a =0; следовательно, cos a = 1. Тогда = D.

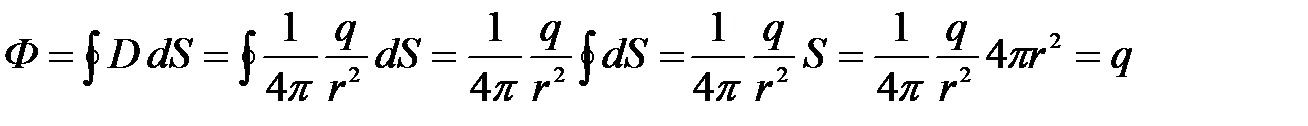
Теорему Гаусса можно записать в виде: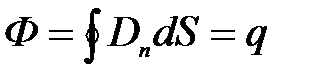

Если поле создается несколькими зарядами, то .

Теорема Гаусса: поток вектора электрического смещения через любую замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности.

Поиск по сайту: