 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Построение изображений в линзах
Прозрачные тела, ограниченные с обеих сторон частями сферических поверхностей, называются линзами. Частный случай – одна из поверхностей плоская. Прямая, проходящая через центры кривизны поверхностей линзы, называется главной оптической осью.
Если С1С2<<R1, R2, то линза называется тонкой. В этом случае точки С1 и С2 (рис.17.1) стремятся к одной точке, называемой оптическим центром линзы (О). Любой луч, проходящий через эту точку, не изменяет своего направления и называется побочной оптической осью. Линза, превращающая световой пучок в сходящийся, называется собирающей. Линза, превращающая световой пучок в расходящийся, называется 
рассеивающей. Виды линз приведены на рис.17.2.. Такие линзы будут собирающими или рассеивающими при условии: показатель преломления (ncр<nл) окружающей среды меньше показателя преломления линзы.
Световые пучки, падающие на линзу, преломляются на обеих поверхностях линзы. Ф ормула тонкой линзы:
(17.1)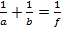 
В данном соотношении а 1– расстояние от предмета до оптического центра линзы, а 2 – расстояние от линзы до изображения, R 1, R 2–радиусы кривизны поверхностей линзы; 
– относительный показатель преломления линзы относительно окружающей среды. Правая часть формулы (4.1) обозначается буквой D и называется оптической силой линзы:
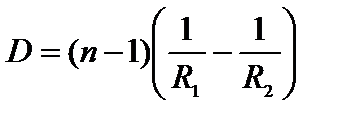, (17.2)
D >0 для собирающей линзы, D <0 для рассеивающей линзы.
Лучи, падающие на тонкую линзу параллельно главной оптической оси, после преломления в собирающей линзе проходят через одну точку, называемую фокусом линзы. Для рассеивающей линзы преломленные лучи идут так, что их продолжения проходят через фокус.
У линз два фокуса (согласно принципа взаимно обратимости световых лучей). Плоскость, проходящая через фокус перпендикулярно главной оптической оси, называется фокальной плоскостью.
Пучок параллельных лучей, падающих на собирающую линзу, после преломления проходит через точку F’ в фокальной плоскости, через которую проходит побочная оптическая ось, параллельная данному пучку (рис.17.3) Если на линзу падает параллельный пучок, то а 1®¥, а 2= F, тогда из соотношений (17.1) и (17.2) следует:
(17.3)
Оптическая сила линзы – это величина, обратная фокусному расстоянию. Измеряется оптическая сила в диоптриях. Оптической силой в 1 дптр обладает линза с фокусным расстоянием равным 1 м.
Для построения изображений в линзах также пользуются «удобными» лучами, ход которых после преломления известен (рис.18.4).
1-1’ – луч, параллельный главной оптической оси, после преломления идет через фокус (для рассеивающей линзы продолжение преломленного луча идет через фокус); 2-2’ – луч, идущий через оптический центр, не меняет своего направления; 3-3’ – луч, идущий через фокус линзы, после преломления идет параллельно главной оптической оси.
Примеры построения изображений приведены на рис. 17.5 и 17.6.
Так как изображение, даваемое линзой, может быть увеличенным или уменьшенным, то отношение размеров изображения к размерам предмета называется линейным или поперечным увеличением:
(17.5)
Из рис.17.5 видно, что DОАВ ~ DОА’В’. Поэтому 
.
Поиск по сайту: