Будущая стоимость постоянной ренты постнумерандо

Поскольку обобщающие характеристики постоянных рент играют существенную роль в анализе финансовых опе­раций, получим формулы для расчета будущей стоимости всех видов постоянных рент, хо­тя для понимания существа дела достаточно разобраться с расчетом соответствующих характеристик годовой ренты.

Годовая рента. Начнем с наиболее простого случая – годовой рен­ты постнумерандо. Пусть в течение n лет в банк в конце каждого года вносится по Rруб. На взносы начисляются сложные процен­ты по ставке i% годовых. Таким образом, имеется рента, член кото­рой равен R, а срок n.Все члены ренты, кроме последнего, прино­сят проценты – на первый член проценты начисляются n - 1 год, на второй n- 2и т.д. На последний взнос проценты не начисля­ются (напомним, что рента постнумерандо). Наращенные к концу срока каждого взноса суммы составят:

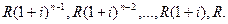
Перепишем этот ряд в обратном порядке. Нетрудно убедиться в том, что он представляет собой геометрическую прогрессию со зна­менателем (1 + i) и первым членом R.Число членов прогрессии рав­но n.Искомая величина равна сумме членов этой про­грессии. Отсюда будущая стоимость финансовой ренты рассчитывается по формуле:

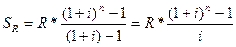
Схема расчета будущей стоимости финансовой ренты постнумерандо (рента, платежи по которой осуществляются в конце периода) представлена на рис. 6.

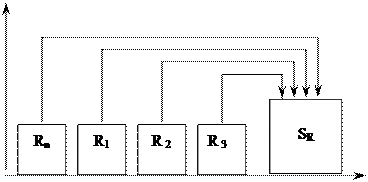время

Рис. 6. Схема расчета будущей стоимости финансовой ренты

Пример 23. На счет в банке в течении пяти лет в конце каждого года будут вноситься суммы в размере 500 рублей, на которые будут начисляться проценты по ставке 30%. Определить сумму процентов, которую банк выплатит владельцу счета.

Решение:

Поскольку период ренты равен одному году, то это годовая рента (проценты начисляются один раз в год); взносы будут в конце периода ренты, значит это рента постнумерандо; сумма платежа постоянна на протяжении всего срока ренты, что характерно для постоянной ренты; число членов ренты пять, т.е. конечно, следовательно, ограниченная рента; а выплаты носят безусловный характер, таким образом, это верная рента.

Сумма всех взносов с начисленными процентами будет равна:

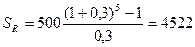руб.

Сумма взносов в течение 5 лет составит:

P = n * R = 5 * 500 = 2500 руб.

Следовательно, сумма начисленных процентов будет равна:

I = S - P = 4522 - 2500 = 2022 руб.

Таким образом, доход владельца счета за 5 лет составит 2022 руб.

Величина ренты при заданной наращенной (будущей) стоимости определяется по формуле:

,

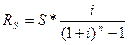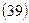
где R_S – величина ренты.

Пример 24. Для покупки автомобиля через 5 лет потребуется 50000 рублей. Определите размер ежегодных взносов, вносимых в конце каждого года в банк, который начисляет проценты по ставке 40%.

Решение:

В данном случае известна наращенная величина постоянной финансовой ренты, поэтому размер ежегодных взносов будет равен:

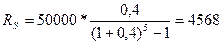руб.

Таким образом, чтобы накопить на счете необходимую сумму для покупки автомобиля следует в конце каждого года в течении пяти лет откладывать 4568 рублей.

Годовая рента, начисление процентов mраз в году. Пусть анализируется годовая рента постнумерандо. Однако проценты на­числяются mраз в году. Члены ренты с начисленными к концу сро­ка процентами образуют ряд (перепишем его в обратном порядке):

,

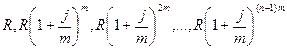где j– номинальная ставка процентов.

И в этом случае мы имеем дело с возрас­тающей геометрической прогрессией. Первый член прогрессии равен R,знаменатель – (1 +j/m)^m.Сумма членов этой прогрессии равна

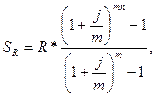
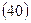
где n – срок ренты.

Пример 25. По данным примера 23, изменив условия: проценты начисляются поквартально.

Решение:

В этом случае рента с начислением процентов 4 раза в год, а общее количество начислений составит 20 раз. Отсюда сумма всех взносов с начисленными на них процентами будет равна:

руб.

Отсюда сумма начисленных процентов будет равна:

I = S - P = 4841 - 2500,00 = 2341 руб.

Как видим, переход от годового начисления процентов к ежеквартальному начислению заметно увеличил как наращенную сумму, так и сумму процентов.

Рента р-срочная (m = 1). Пусть рента выплачивается рраз в году рав­ными суммами, процент начисляется один раз в конце года. Если годовая сумма платежей равна R, то каждый раз выплачивается R/p.Общее число членов ренты равно n*р.Ряд членов ренты с начислен­ными процентами представляет собой геометрическую прогрессию. Первый член ее равен R/p,знаменатель – (1 + i)^1/p. Наращенная сумма членов этой прогрессии:

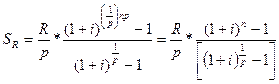
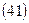
где р – количество выплат в году.

Рента р-срочная (p = m). На практике часто встречаются случаи, ко­гда число выплат в году равно числу начислений процентов, т.е. когда р = m.Для получения необходимой формулы воспользуемся формулой 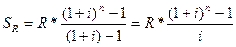, в которой i заменяется на j/m,а вместо числа лет берется число периодов выплат ренты n*р,член ренты равен R/p.Поскольку р = m, то в итоге получим:

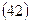
Искомая величина может быть получена и по формуле .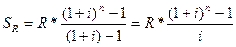

В этом случае вместо числа лет подставляем в формулу число перио­дов, а вместо годового члена ренты – выплату за период, кроме то­го, вместо годовой ставки берется ставка за период.

Рента р-срочная (p m). Определим теперь будущую стоимость для наиболее общего случая – р-срочная рента с начислением процен­тов mраз в году, т.е. когда рентные платежи вносятся несколько раз в году и начисление процентов также происходит несколько раз в год, но число рентных платежей не равно числу периодов начисления процентов. Общее количество членов ренты равно n*р,вели­чина члена ренты R/p.Члены ренты с начисленными процентами образуют ряд, следующий геометрической прогрессии, с первым членом R/pи знаменателем (1 + j/m)^m/p. Сумма членов такой про­грессии составит:

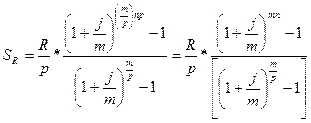
Поиск по сайту: