 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Современная стоимость постоянной ренты постнумерандо. Cовременная стоимость потока платежей – сумма дисконтированных членов этого потока на некоторый предшествующий момент времени
Cовременная стоимость потока платежей – сумма дисконтированных членов этого потока на некоторый предшествующий момент времени. Вместо терминов «современная стоимость» и «современная величина» потока платежей в зависимости от контекста употребляют термины текущая стоимость и приведенная величина. Современная стоимость потока платежей эквивалентна в финансовом смысле всем платежам, которые охватывает поток. Методы расчета современных стоимостей финансовых рент обсудим в том же порядке, что и методы наращения рент.
Годовая рента. Начнем с самого простого случая – годовой ренты постнумерандо, член которой равен R,срок ренты n, ежегодное дисконтирование. Обозначим сумму членов этой прогрессии как Р. Найдем ее:
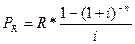
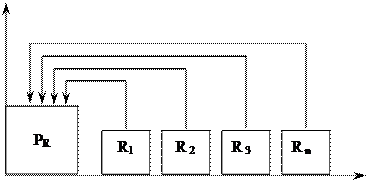
Схема расчета современной стоимости финансовой ренты постнумерандо представлена на рис. 7.
 | |||
 | |||
время
Рис. 7. Схема расчета современной стоимости финансовой ренты
Заметим, что эта формула применяется и для определения современной стоимости р-срочной ренты. В этом случае переменная n означает число периодов, а i – ставку за период (но не годовую ставку).
Финансовая рента (аннуитет), особенно его современная стоимость, широко применяются в различных финансовых расчетах:
ü разработка плана последовательного погашения задолженности;
ü измерение финансовой эффективности проекта;
ü лизинговые расчеты;
ü оценка имущества;
ü расчеты по накопительному пенсионному страхованию;
ü расчеты по ипотеке;
ü расчеты по договору ренты;
ü расчеты по договору пожизненного содержания с иждивением;
ü расчеты по коммерческому кредиту (рассрочка платежа).
Ипотека – долгосрочный кредит, выдаваемый под залог недвижимости.
Определение (ГК РФ ст. 583). По договору ренты одна сторона (получатель ренты) передает другой стороне (плательщику ренты) в собственность имущество, а плательщик ренты обязуется в обмен на полученное имущество периодически выплачивать получателю ренту в виде определенной денежной суммы либо предоставления средств на его содержание в иной форме.
Определение (ГК РФ ст. 601). По договору пожизненного содержания с иждивением получатель ренты – гражданин передает принадлежащие ему жилой дом, квартиру, земельный участок или иную недвижимость в собственность плательщика ренты, который обязуется осуществлять пожизненное содержание с иждивением гражданина и (или) указанного им третьего лица.
Определение (ГК РФ ст. 823). Договором... может предусматриваться предоставление кредита, в том числе в виде аванса, предварительной оплаты, отсрочки и рассрочки оплаты товаров, работ или услуг (коммерческий кредит).
Пример 26. По данным примера 23 определить современную стоимость ренты.
Решение:
Современная величина ренты составит:
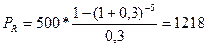 руб.
руб.
Таким образом, все производимые в будущем платежи оцениваются в настоящий момент в размере 1218 руб.
Величина ренты при заданной современной стоимости определяется по формуле:
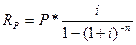 ,
, 
где RР – величина ренты.
Пример 27. Рассчитайте стоимость имущества, которая приносит ежегодный доход 200 руб. в течение 5 лет. Годовой процент 10%.
Решение:
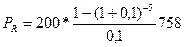 руб.
руб.
Пример 28. Рассчитайте периодические платежи по договору лизинга, если стоимость приобретаемого имущества 1 млн. рублей, лизинговый процент 20% годовых, срок лизинга 3 года, платеж ежеквартальный.
Решение:
 руб.
руб.
Пример 29. Ежегодно работник вносит 1000 рублей в накопительный пенсионный фонд на протяжении 20 лет. Сколько он затем сможет получать ежегодно из фонда на протяжении следующих 20 лет, если деньги помещаются фондом под 5% годовых.
Решение:
На первом этапе расчетов используется формула будущей стоимости ренты, на втором - формула, производная от формулы современной стоимости ренты:
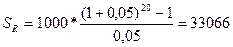 руб.
руб.
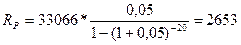 руб.
руб.
Пример 30. Будущая стоимость недвижимости, передаваемой по договору пожизненного содержания, 500000 рублей. Рассчитайте величину ежемесячной ренты, выплачиваемой в течение 20 лет, если ежегодный процент 10%.
Решение:
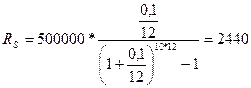 руб.
руб.
Годовая рента, начисление процентов mраз в году. Заменим в выше приведенной формуле дисконтный множитель (1 + i)-n на эквивалентную величину (1 + j/m)-mn,соответственно i заменим на (1 + j/m)m - 1, после чего имеем:

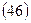
Рента р-срочная (m = 1). Если платежи производятся не один, а рраз в году, то коэффициенты приведения находятся так же, как и в случае годовой ренты. Только теперь размер платежа равен R/p,а число членов n*р.Сумма дисконтированных платежей равна:
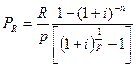
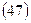
Рента р-срочная (p = m). Число членов ренты здесь равно числу начислений процентов, величина члена ренты составляет R/m.В итоге:
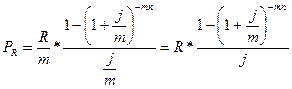

Искомый результат можно получить и по формуле 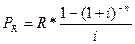 и при этом воспользоваться таблицей коэффициентов приведения постоянных рент. В этом случае вместо числа лет берется количество периодов ренты, процентная ставка и величина члена ренты определяются соответствующим образом.
и при этом воспользоваться таблицей коэффициентов приведения постоянных рент. В этом случае вместо числа лет берется количество периодов ренты, процентная ставка и величина члена ренты определяются соответствующим образом.
Рента р-срочная (p  m). Сумма членов соответствующей прогрессии составит:
m). Сумма членов соответствующей прогрессии составит:
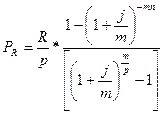
Поиск по сайту: